
【题目】已知f(x)=ln(ax+b)+x2(a≠0).
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=x,求a,b的值;
(2)若f(x)≤x2+x恒成立,求ab的最大值.
【答案】
(1)解:∵f(x)=ln(ax+b)+x2(a≠0),
∴ ![]() ,
,
∵曲线y=f(x)在点(1,f(1))处的切线方程为y=x,
∴ 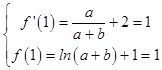 ,
,
解得,a=﹣1,b=2;
(2)解:设g(x)=f(x)﹣(x2+x),则g(x)=ln(ax+b)﹣x,依题意g(x)≤0恒成立,
①a<0时,g(x)定义域 ![]() ,
,
取x0使得 ![]() ,得
,得 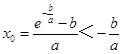 ,
,
则 ![]()
与g(x)≤0矛盾,∴a<0不符合要求,
②a>0时, 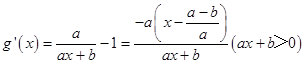 ,
,
当 ![]() 时,g'(x)>0;当
时,g'(x)>0;当 ![]() 时,g'(x)<0,
时,g'(x)<0,
∴g(x)在区间 ![]() 上为增函数,在区间
上为增函数,在区间 ![]() 上为减函数,
上为减函数,
∴g(x)在其定义域 ![]() 上有最大值,最大值为
上有最大值,最大值为 ![]() ,
,
由g(x)≤0,得 ![]() ,∴b≤a﹣alna,∴ab≤a2﹣a2lna,
,∴b≤a﹣alna,∴ab≤a2﹣a2lna,
设h(a)=a2﹣a2lna,则h'(a)=2a﹣(2alna+a)=a(1﹣2lna),
∴ ![]() 时,
时, ![]() 时,h'(a)<0,
时,h'(a)<0,
∴h(a)在区间 ![]() 上为增函数,在区间
上为增函数,在区间 ![]() 上为减函数,
上为减函数,
∴h(a)的最大值为 ![]() ,
,
∴当 ![]() 时,ab取最大值为
时,ab取最大值为 ![]() ,
,
综合①,②得,ab最大值为 ![]() .
.
【解析】(1)推导出 ![]() ,利用导数的几何意义列出方程组,能求出a,b的值.(2)设g(x)=f(x)﹣(x2+x),则g(x)=ln(ax+b)﹣x,依题意g(x)≤0恒成立,根a<0,a>0两种情况分类讨论,利用导数性质能求出ab的最大值.
,利用导数的几何意义列出方程组,能求出a,b的值.(2)设g(x)=f(x)﹣(x2+x),则g(x)=ln(ax+b)﹣x,依题意g(x)≤0恒成立,根a<0,a>0两种情况分类讨论,利用导数性质能求出ab的最大值.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC=(3a﹣c)cosB.D为AC边的中点,且BD=1,则△ABD面积的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即S= ![]() .现有周长为2
.现有周长为2 ![]() +
+ ![]() 的△ABC满足sinA:sinB:sinC=(
的△ABC满足sinA:sinB:sinC=( ![]() ﹣1):
﹣1): ![]() :(
:( ![]() +1),试用以上给出的公式求得△ABC的面积为( )
+1),试用以上给出的公式求得△ABC的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ax﹣1)e2x+x+1(其中e为自然对数的e底数).
(1)若a=0,求函数f(x)的单调区间;
(2)对x∈(0,+∞),f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 抛物线
抛物线 ![]() 焦点均在
焦点均在 ![]() 轴上,
轴上, ![]() 的中心和
的中心和 ![]() 顶点均为原点
顶点均为原点 ![]() ,从每条曲线上各取两个点,将其坐标记录于表中,则
,从每条曲线上各取两个点,将其坐标记录于表中,则 ![]() 的左焦点到
的左焦点到 ![]() 的准线之间的距离为( )
的准线之间的距离为( )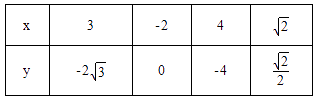
A.![]()
B.![]()
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列 ![]() 满足:①
满足:① ![]() ;②所有项
;②所有项 ![]() ;③
;③ ![]() .
.
设集合 ![]() ,将集合
,将集合 ![]() 中的元素的最大值记为
中的元素的最大值记为 ![]() .换句话说,
.换句话说, ![]() 是
是
数列 ![]() 中满足不等式
中满足不等式 ![]() 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列 ![]() 为数列
为数列 ![]() 的
的
伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)若数列 ![]() 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列 ![]() ;
;
(2)设 ![]() ,求数列
,求数列 ![]() 的伴随数列
的伴随数列 ![]() 的前100之和;
的前100之和;
(3)若数列 ![]() 的前
的前 ![]() 项和
项和 ![]() (其中
(其中 ![]() 常数),试求数列
常数),试求数列 ![]() 的伴随数列
的伴随数列 ![]() 前
前 ![]() 项和
项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且S3=9,a2a4=21,数列{bn}满足 ![]() ,若
,若 ![]() ,则n的最小值为( )
,则n的最小值为( )
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某商品每吨的价格为x(1<x<14)万元时,该商品的月供给量为y1吨,y1=ax+ ![]() a2﹣a(a>0):月需求量为y2吨,y2=﹣
a2﹣a(a>0):月需求量为y2吨,y2=﹣ ![]() x2﹣
x2﹣ ![]() x+1,当该商品的需求量大于供给量时,销售量等于供给量:当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
x+1,当该商品的需求量大于供给量时,销售量等于供给量:当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.
(1)已知a= ![]() ,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
,若某月该商品的价格为x=7,求商品在该月的销售额(精确到1元);
(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6万元,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com