Question

【题目】设点、是平面上左、右两个不同的定点， ，动点满足：

．

（1）求证：动点的轨迹为椭圆；

（2）抛物线满足：①顶点在椭圆的中心；②焦点与椭圆的右焦点重合．

设抛物线与椭圆的一个交点为．问：是否存在正实数，使得的边长为连续自然数．若存在，求出的值；若不存在，说明理由．

Answer 1

【答案】（1）见解析；（2）存在实数，使得的边长为连续自然数。

【解析】试题分析: （1）根据题意，分两种情况讨论：①点P、F1、F2构成三角形，②点P、F1、F2不构成三角形，每种情况下分析可得|PF1|+|PF2|=4m，由椭圆的定义分析可得答案；

（2）根据题意，由（1）可得，动点P的轨迹方程，分析可得抛物线的焦点坐标，假设存在满足条件的实数m，结合椭圆与抛物线的性质分析可得m的值，即可得答案．

试题解析

（1）若点构成三角形则

，

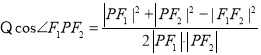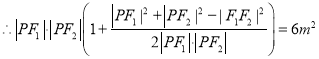
整理得，即．

若点不构成三角形，也满足．

所以动点的轨迹为椭圆

（2）动点的轨迹方程为

抛物线的焦点坐标为与椭圆的右焦点重合．

假设存在实数，使得的边长为连续自然数．

因为，

不妨设|，

由抛物线的定义可知，解得，

设点的坐标为，

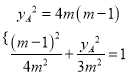
整理得，解得或

所以存在实数，使得的边长为连续自然数