
【题目】已知![]() 是无穷数列.给出两个性质:
是无穷数列.给出两个性质:
①对于![]() 中任意两项
中任意两项![]() ,在
,在![]() 中都存在一项
中都存在一项![]() ,使
,使![]() ;
;
②对于![]() 中任意项
中任意项![]() ,在
,在![]() 中都存在两项
中都存在两项![]() .使得
.使得![]() .
.
(Ⅰ)若![]() ,判断数列
,判断数列![]() 是否满足性质①,说明理由;
是否满足性质①,说明理由;
(Ⅱ)若![]() ,判断数列
,判断数列![]() 是否同时满足性质①和性质②,说明理由;
是否同时满足性质①和性质②,说明理由;
(Ⅲ)若![]() 是递增数列,且同时满足性质①和性质②,证明:
是递增数列,且同时满足性质①和性质②,证明:![]() 为等比数列.
为等比数列.
【答案】(Ⅰ)详见解析;(Ⅱ)详解解析;(Ⅲ)证明详见解析.
【解析】
(Ⅰ)根据定义验证,即可判断;
(Ⅱ)根据定义逐一验证,即可判断;
(Ⅲ)解法一:首先,证明数列中的项数同号,然后证明![]() ,最后,用数学归纳法证明数列为等比数列即可.
,最后,用数学归纳法证明数列为等比数列即可.
解法二:首先假设数列中的项数均为正数,然后证得![]() 成等比数列,之后证得
成等比数列,之后证得![]() 成等比数列,同理即可证得数列为等比数列,从而命题得证.
成等比数列,同理即可证得数列为等比数列,从而命题得证.
(Ⅰ)![]() 不具有性质①;
不具有性质①;
(Ⅱ)![]() 具有性质①;
具有性质①;
![]() 具有性质②;
具有性质②;
(Ⅲ)解法一
首先,证明数列中的项数同号,不妨设恒为正数:
显然![]() ,假设数列中存在负项,设
,假设数列中存在负项,设![]() ,
,
第一种情况:若![]() ,即
,即![]() ,
,
由①可知:存在![]() ,满足
,满足![]() ,存在
,存在![]() ,满足
,满足![]() ,
,
由![]() 可知
可知![]() ,从而
,从而![]() ,与数列的单调性矛盾,假设不成立.
,与数列的单调性矛盾,假设不成立.
第二种情况:若![]() ,由①知存在实数
,由①知存在实数![]() ,满足
,满足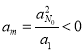 ,由
,由![]() 的定义可知:
的定义可知:![]() ,
,
另一方面,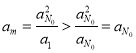 ,由数列的单调性可知:
,由数列的单调性可知:![]() ,
,
这与![]() 的定义矛盾,假设不成立.
的定义矛盾,假设不成立.
同理可证得数列中的项数恒为负数.
综上可得,数列中的项数同号.
其次,证明![]() :
:
利用性质②:取![]() ,此时
,此时![]() ,
,
由数列的单调性可知![]() ,
,
而![]() ,故
,故![]() ,
,
此时必有![]() ,即
,即![]() ,
,
最后,用数学归纳法证明数列为等比数列:
假设数列![]() 的前
的前![]() 项成等比数列,不妨设
项成等比数列,不妨设![]() ,
,
其中![]() ,(
,(![]() 的情况类似)
的情况类似)
由①可得:存在整数![]() ,满足
,满足![]() ,且
,且![]() (*)
(*)
由②得:存在![]() ,满足:
,满足:![]() ,由数列的单调性可知:
,由数列的单调性可知:![]() ,
,
由![]() 可得:
可得:![]() (**)
(**)
由(**)和(*)式可得:![]() ,
,
结合数列的单调性有:![]() ,
,
注意到![]() 均为整数,故
均为整数,故![]() ,
,
代入(**)式,从而![]() .
.
总上可得,数列![]() 的通项公式为:
的通项公式为:![]() .
.
即数列![]() 为等比数列.
为等比数列.
解法二:
假设数列中的项数均为正数:
首先利用性质②:取![]() ,此时
,此时![]() ,
,
由数列的单调性可知![]() ,
,
而![]() ,故
,故![]() ,
,
此时必有![]() ,即
,即![]() ,
,
即![]() 成等比数列,不妨设
成等比数列,不妨设![]() ,
,
然后利用性质①:取![]() ,则
,则![]() ,
,
即数列中必然存在一项的值为![]() ,下面我们来证明
,下面我们来证明![]() ,
,
否则,由数列的单调性可知![]() ,
,
在性质②中,取![]() ,则
,则![]() ,从而
,从而![]() ,
,
与前面类似的可知则存在![]() ,满足
,满足![]() ,
,
若![]() ,则:
,则:![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,则:
,则:![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,则:
,则:![]() ,与数列的单调性矛盾;
,与数列的单调性矛盾;
即不存在满足题意的正整数![]() ,可见
,可见![]() 不成立,从而
不成立,从而![]() ,
,
然后利用性质①:取![]() ,则数列中存在一项
,则数列中存在一项![]() ,
,
下面我们用反证法来证明![]() ,
,
否则,由数列的单调性可知![]() ,
,
在性质②中,取![]() ,则
,则![]() ,从而
,从而![]() ,
,
与前面类似的可知则存在![]() ,满足
,满足![]() ,
,
即由②可知:![]() ,
,
若![]() ,则
,则![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,则
,则![]() ,与假设矛盾;
,与假设矛盾;
若![]() ,由于
,由于![]() 为正整数,故
为正整数,故![]() ,则
,则![]() ,与
,与![]() 矛盾;
矛盾;
综上可知,假设不成立,则![]() .
.
同理可得:![]() ,从而数列
,从而数列![]() 为等比数列,
为等比数列,
同理,当数列中的项数均为负数时亦可证得数列为等比数列.
由推理过程易知数列中的项要么恒正要么恒负,不会同时出现正数和负数.
从而题中的结论得证,数列![]() 为等比数列.
为等比数列.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙两名医生,抽调![]() 、
、![]() 、
、![]() 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士
三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士![]() 被选在第一医院工作的概率为( )
被选在第一医院工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

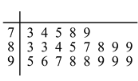
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() ,点
,点![]() 是抛物线
是抛物线![]() 的焦点,过点F作直线
的焦点,过点F作直线![]() 交抛物线于M,N两点,延长
交抛物线于M,N两点,延长![]() ,
,![]() 分别交椭圆于A,B两点,记
分别交椭圆于A,B两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,
,![]() .
.
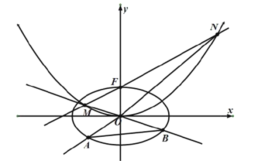
(1)求![]() 的值及抛物线的准线方程;
的值及抛物线的准线方程;
(2)求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右两个焦点为
的左,右两个焦点为![]() 、
、![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 有公共焦点
有公共焦点![]() .且两曲线
.且两曲线![]() 、
、![]() 在第一象限的交点
在第一象限的交点![]() 的横坐标为
的横坐标为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 的交点为
的交点为![]() 、
、![]() (
(![]() 为坐标原点),与椭圆
为坐标原点),与椭圆![]() 的交点为
的交点为![]() 、
、![]() (
(![]() 在线段
在线段![]() 上),且
上),且![]() .问满足条件的直线
.问满足条件的直线![]() 有几条,说明理由.
有几条,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级进行选课走班,已知语文、数学、英语是必选学科,另外需从物理、化学、生物、政治、历史、地理6门学科中任选3门进行学习. 现有甲、乙、丙三人,若同学甲必选物理,则下列结论正确的是( )
A.甲的不同的选法种数为10
B.甲、乙、丙三人至少一人选化学与全选化学是对立事件
C.乙同学在选物理的条件下选化学的概率是![]()
D.乙、丙两名同学都选物理的概率是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最大值为
的最大值为![]() ;
;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 在区间
在区间![]() 单调递增.
单调递增.
其中所有正确结论的编号是( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对n个不同的实数a1,a2,…,an可得n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i行ai1,ai2,…,ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnain,i=1,2,3…,n!.例如用1,2,3可得数阵如图,对于此数阵中每一列各数之和都是12,所以bl+b2+…b6=-12+2×12-3×12=-24.那么,在用1,2,3,4,5形成的数阵中,b1+b2+…b120等于( )

A.-3600B.-1800C.-1080D.-720
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com