
【题目】设f(x)是定义在实数集R上的函数,满足条件y=f(x+1)是偶函数,且当x≥1时,f(x)= ![]() ,则
,则 ![]() 的大小关系是( )
的大小关系是( )
A.![]()
B.![]()
C.![]()
D.![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设甲、乙两人每次射击命中目标的概率分别为 ![]() ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗.2018年春节前夕, ![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,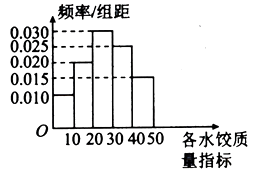
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值 ![]() 服从正态分布
服从正态分布 ![]() ,利用该正态分布,求
,利用该正态分布,求 ![]() 落在
落在 ![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于 ![]() 内的包数为
内的包数为 ![]() ,求
,求 ![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为 ![]() ;
;
②若 ![]() ,则
,则 ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 点(n,Sn+3)(n∈N*)在函数y=3×2x的图象上,等比数列{bn}满足bn+bn+1=an(n∈N*).其前n项和为Tn , 则下列结论正确的是( )
A.Sn=2Tn
B.Tn=2bn+1
C.Tn>an
D.Tn<bn+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-e-x(x∈R,且e为自然对数的底数).
(1)判断函数f(x)的单调性与奇偶性;
(2)是否存在实数t , 使不等式f(x-t)+f(x2-t2)≥0对一切x∈R都成立?若存在,求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上动点 ![]() 与两个定点
与两个定点 ![]() ,
, ![]() ,且
,且 ![]() .
.
(1)求点 ![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中轨迹为 ![]() ,过点
,过点 ![]() 的直线
的直线 ![]() 被
被 ![]() 所截得的线段长度为8,求直线
所截得的线段长度为8,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() ,设
,设 ![]() .
.
(Ⅰ)若f(α)=2,求 ![]() 的值;
的值;
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a﹣b)cosC=ccosB,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂为预测产品的回收率 ![]() ,需要研究它和原料有效成分含量
,需要研究它和原料有效成分含量 ![]() 之间的相关关系,现收集了4组对照数据。
之间的相关关系,现收集了4组对照数据。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请根据相关系数 ![]() 的大小判断回收率
的大小判断回收率 ![]() 与
与 ![]() 之间是否存在高度线性相关关系;
之间是否存在高度线性相关关系;
(Ⅱ)请根据上表提供的数据,用最小二乘法求出 ![]() 关于
关于 ![]() 的线性回归方程
的线性回归方程 ![]() ,并预测当
,并预测当 ![]() 时回收率
时回收率 ![]() 的值.
的值.
参考数据: 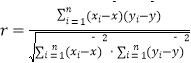
| 1 | 0 |
|
| 其他 |
| 完全相关 | 不相关 | 高度相关 | 低度相关 | 中度相关 |
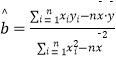 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com