
【题目】如图,在几何体![]() 中,四边形
中,四边形![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(Ⅰ)见证明(Ⅱ)![]()
【解析】
(Ⅰ)取AE的中点H,连接HG,HD,通过证明四边形HGFD是平行四边形来证明GF∥DH,由线面平行的判定定理可得;
(Ⅱ)以B为原点,分别以![]() 的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,可得平面BEC和平面AEF的法向量,由向量夹角的余弦值可得.
的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,可得平面BEC和平面AEF的法向量,由向量夹角的余弦值可得.
(Ⅰ)如图,取![]() 的中点
的中点![]() 连接
连接![]() ,
,![]() ,又
,又![]() 是
是![]() 的中点,
的中点,
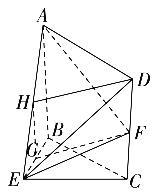
所以![]() ,且
,且![]() ,
,
又![]() 是
是![]() 中点,所以
中点,所以![]() ,
,
由四边形![]() 是矩形得,
是矩形得,![]() ,
,![]() ,
,
所以![]() 且
且![]() .
.
从而四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
∵DH平面ADE,GF平面ADE,∴GF∥平面ADE.
(Ⅱ)如图,在平面![]() 内,过点
内,过点![]() 作
作![]() ,因为
,因为![]() ,所以
,所以![]() .又
.又![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() .
.
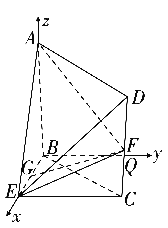
以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,设
轴的正方向建立空间直角坐标系,设![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的法向量,设
的法向量,设![]() 为平面
为平面![]() 的法向量. 又
的法向量. 又![]() ,
,![]()
 ,即
,即![]() ,取
,取![]() ,
,
![]() ,
, ,
,
所以平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】对于复数![]() (
(![]()
![]() 为虚数单位),定义
为虚数单位),定义![]() ,给出下列命题:①对任何复数z,都有
,给出下列命题:①对任何复数z,都有![]() ,等号成立的充要条件是
,等号成立的充要条件是![]() ;②
;②![]() :③若
:③若![]() ,则
,则![]() :④对任何复数
:④对任何复数![]()
![]()
![]() ,不等式
,不等式![]() 恒成立,其中真命题的个数是( )
恒成立,其中真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() :
:![]() ,圆
,圆![]() :
:![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求圆![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的点,若
上的点,若![]() 为等边三角形,求
为等边三角形,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]()
![]() ,焦点
,焦点![]() ,如果存在过点
,如果存在过点![]()
![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() .
.![]() ,使得
,使得![]() ,则称点
,则称点![]() 为抛物线
为抛物线![]() 的“
的“![]() 分点”.
分点”.
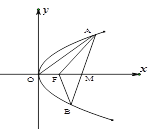
(1)如果![]() ,直线
,直线![]() :
:![]() ,求
,求![]() 的值;
的值;
(2)如果![]() 为抛物线
为抛物线![]() 的“
的“![]() 分点”,求直线
分点”,求直线![]() 的方程;
的方程;
(3)证明点![]() 不是抛物线
不是抛物线![]() 的“2分点”;
的“2分点”;
(4)如果![]()
![]() 是抛物线的“2分点”,求
是抛物线的“2分点”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=m,点M是棱CD的中点.
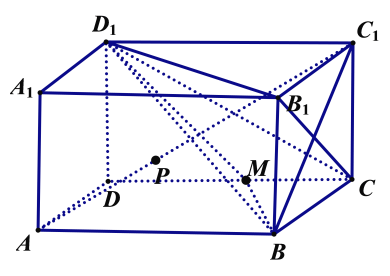
(1)求异面直线B1C与AC1所成的角的大小;
(2)是否存在实数m,使得直线AC1与平面BMD1垂直?说明理由;
(3)设P是线段AC1上的一点(不含端点),满足![]() λ,求λ的值,使得三棱锥B1﹣CD1C1与三棱锥B1﹣CD1P的体积相等.
λ,求λ的值,使得三棱锥B1﹣CD1C1与三棱锥B1﹣CD1P的体积相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹,用于装点生活或配合其他民俗活动的民间艺术;蕴含了极致的数学美和丰富的传统文化信息,现有一幅剪纸的设计图,其中的4个小圆均过正方形的中心,且内切于正方形的两邻边.若在正方形内随机取一点,则该点取自黑色部分的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为
所表示的曲线为![]() ,则下面四个选项中错误的是( )
,则下面四个选项中错误的是( )
A.若![]() 为椭圆,则
为椭圆,则![]() B.若
B.若![]() 是双曲线,则其离心率有
是双曲线,则其离心率有![]()
C.若![]() 为双曲线,则
为双曲线,则![]() 或
或![]() D.若
D.若![]() 为椭圆,且长轴在
为椭圆,且长轴在![]() 轴上,则
轴上,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若公差为![]() 的无穷等差数列
的无穷等差数列![]() 的前
的前![]() 项和为
项和为![]() ,则下列说法:(1)若
,则下列说法:(1)若![]() ,则数列
,则数列![]() 有最大项;(2)若数列
有最大项;(2)若数列![]() 有最大项,则
有最大项,则![]() ;(3)若数列
;(3)若数列![]() 是递增数列,则对任意
是递增数列,则对任意![]() 都有
都有![]() ;(4)若对任意
;(4)若对任意![]() 都有
都有![]() ,则数列
,则数列![]() 是递增数列;其中正确的是______.(选序号).
是递增数列;其中正确的是______.(选序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com