
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 和
和![]() 两点.
两点.
(1)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)若过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,记
两点,记![]() 与
与![]() 的面积分别为
的面积分别为![]() 与
与![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,列出韦达定理,结合条件
的方程联立,列出韦达定理,结合条件![]() 可求得
可求得![]() 的值,进而可求得直线
的值,进而可求得直线![]() 的方程;
的方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立,列出韦达定理,利用弦长公式求得
的方程联立,列出韦达定理,利用弦长公式求得![]() ,利用三角形的面积公式可求得
,利用三角形的面积公式可求得![]() ,同理可得出
,同理可得出![]() 的表达式,然后利用基本不等式可求得
的表达式,然后利用基本不等式可求得![]() 的最小值.
的最小值.
(1)直线![]() 过的定点
过的定点![]() 在横轴上,且直线
在横轴上,且直线![]() 与抛物线相交,则斜率一定不能为
与抛物线相交,则斜率一定不能为![]() ,所以可设直线
,所以可设直线![]() 方程为
方程为![]() .
.
联立![]() ,消去
,消去![]() 得
得![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
所以![]() .
.
因为![]() ,所以
,所以![]() ,解得
,解得![]() .
.
所以直线![]() 的方程为
的方程为![]() 或
或![]() ;
;
(2)根据(1),设直线![]() 的方程为
的方程为![]() .
.
联立![]() ,消去
,消去![]() 得
得![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
则![]()
![]() .
.
因为直线![]() 与直线
与直线![]() 垂直,
垂直,
且当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,则此时直线
,则此时直线![]() 的方程为
的方程为![]() .但此时直线
.但此时直线![]() 与抛物线
与抛物线![]() 没有两个交点,
没有两个交点,
所以不符合题意,所以![]() .
.
所以直线![]() 的斜率为
的斜率为![]() ,可得
,可得![]() ,
,

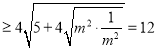 ,
,
当且仅当![]() 时,等号成立,因此,
时,等号成立,因此,![]() 的最小值为
的最小值为![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
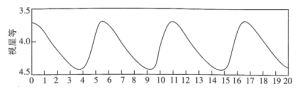
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,雨水、惊蛰、春分、清明日影之和为三丈二尺,前七个节气日影之和为七丈三尺五寸,问谷雨日影长为( )
A.七尺五寸B.六尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有9位身高各异的同学拍照留念,分成前后两排,前排4人,后排5人,要求每排同学的身高从中间到两边依次递减,则不同的排队方式有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 只有一个公共点,点
只有一个公共点,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(1)求抛物线![]() 的方程;
的方程;
(2)①若![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
②若![]() 是抛物线
是抛物线![]() 上与原点不重合的定点,且
上与原点不重合的定点,且![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一排10个位置的空停车场,甲、乙、丙三辆不同的车去停放,要求每辆车左右两边都有空车位且甲车在乙、丙两车之间的停放方式共有_________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com