Question

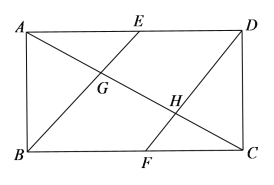
【题目】如图，一张矩形白纸，，，，分别为，的中点，现分别将，沿，DF折起，且、在平面同侧，下列命题正确的是_________（写出所有正确命题的序号）

①平面平面时，

②当平面平面时，平面

③当、重合于点时，

④当、重合于点时，三棱锥的外接球的半径为

Answer 1

【答案】②

【解析】

分别作出平面平面时，、重合于点时几何体图形，根据线面位置关系和长度关系证明判定，利用补图法求外接球的半径．

由题：矩形中，，，，分别为，的中点，

，

所以，同理可得，，

，

中，，所以，

由余弦定理，

当平面平面时，如图：

所以在折叠后的图形中，，

可得平面，平面，由于，

平面与平面都经过，则平面与平面重合，

所以四边形为平行四边形，，平面，平面

所以平面，所以②正确；

假设，则四边形为平行四边形，可得与矛盾，所以①矛盾；

当、重合于点时，如图：

由题可得：，，

，所以不可能，所以③错误；

三棱锥中，，

所以为直角三角形，，

，所以为直角三角形，

为直角三角形，

由补图法可知三棱锥的与以为长宽高的长方体外接球相同，

其直径为，

所以外接球的半径为，所以④不正确；

故答案为：②