
【题目】已知圆![]() :
: ![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,点
轴正半轴的交点,点![]() ,
, ![]() 在曲线
在曲线![]() 上,若直线
上,若直线![]() ,
, ![]() 的斜率分别是
的斜率分别是![]() ,
, ![]() ,满足
,满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)分析条件可得圆心![]() 满足条件
满足条件![]() >
>![]() ,从而可得曲线E是M,N为焦点,长轴长为
,从而可得曲线E是M,N为焦点,长轴长为![]() 的椭圆,可得椭圆的方程;(2)设直线
的椭圆,可得椭圆的方程;(2)设直线![]() 的方程为
的方程为![]() ,代入椭圆方程消去x整理得到关于y的方程,进一步可得
,代入椭圆方程消去x整理得到关于y的方程,进一步可得![]()
![]() ,由
,由![]() 可求得
可求得![]() ,从而
,从而![]() ,从而
,从而
可得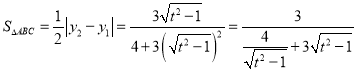
![]() ,从而可得三角形面积的最大值。
,从而可得三角形面积的最大值。
试题解析:
(1)由题意得圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
点![]() 在圆
在圆![]() 内,因为动圆
内,因为动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,所以动圆
相切,所以动圆![]() 与圆
与圆![]() 内切。
内切。
设动圆![]() 半径为
半径为![]() ,则
,则![]()
![]() .
.
因为动圆![]() 经过点
经过点![]() ,所以
,所以![]() ,
, ![]() >
>![]() ,
,
所以曲线E是M,N为焦点,长轴长为![]() 的椭圆.
的椭圆.
设椭圆的方程为![]()
则![]() ,
,
∴![]() ,
,
∴曲线![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 的斜率为0时,不合题意;
的斜率为0时,不合题意;
设直线![]() 的方程为
的方程为![]() ,
,
由 消去x整理得
消去x整理得![]() ,
,
设![]() ,
,
则![]() ,
,
由条件得点A坐标为(1,0),
∵![]() ,
,
∴![]()
=![]() .且
.且![]() ,
,
∴![]() ,
,
解得![]() ,
,
故直线BC过定点(2,0),
由![]() ,解得
,解得![]() ,
,
∴
![]() ,当且仅当
,当且仅当![]() 时取等号。
时取等号。
综上![]() 面积的最大值为
面积的最大值为![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示,⊙O与⊙O′相交于A、B两点,过A引直线CD,EF分别交两圆于点C、D、E、F,EC与DF的延长线相交于点P,求证:∠P+∠CBD=180°.
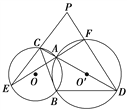
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在梯形BCDE中,BC∥DE,BA⊥DE,且EA=DA=AB=2CB=2,沿AB将四边形ABCD折起,使得平面ABCD与平面ABE垂直,M为CE的中点.
(1)求证:AM⊥BE;
(2)求三棱锥C﹣BED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间计划每天生产卡车模型、赛车模型、小汽车模型这三种玩具共100个,已知生产一个卡车模型需5分钟,生产一个赛车模型需7分钟,生产一个小汽车模型需4分钟,且生产一个卡车模型可获利润8元,生产一个赛车模型可获利润9元,生产一个小汽车模型可获利润6元.若总生产时间不超过10小时,该公司合理分配生产任务使每天的利润最大,则最大利润是______________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差大于零的等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是等差数列,且
是等差数列,且![]() ,求非零常数
,求非零常数![]() 的值.
的值.
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在正整数
项和,是否存在正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 均成立?若存在,求出
均成立?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com