
【题目】如图,在四棱锥![]() 中,底面ABCD为矩形,
中,底面ABCD为矩形,![]() ,
,![]() ,侧面SAD是以AD为斜边的等腰直角三角形,且平面
,侧面SAD是以AD为斜边的等腰直角三角形,且平面![]() 平面ABCD,M,N分别为AD,SC的中点.
平面ABCD,M,N分别为AD,SC的中点.
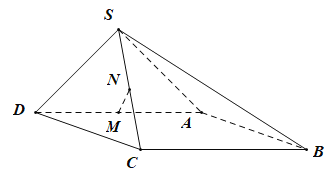
(1)求证:![]() 平面SAB.
平面SAB.
(2)求直线BN与平面SAB所成角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)取SB的中点H,连接AH与NH,由平面几何的知识可得四边形AHNM是平行四边形,![]() ,再由线面平行的判定即可得证;
,再由线面平行的判定即可得证;
(2)设直线BN与平面SAB所成的角为![]() ,其中
,其中![]() ,点N到平面SAB的距离为d,由题意结合线面、面面位置关系的性质与判定可得
,点N到平面SAB的距离为d,由题意结合线面、面面位置关系的性质与判定可得![]() ,连接SM,由面面垂直的性质可得
,连接SM,由面面垂直的性质可得![]() 平面ABCD,进而可得
平面ABCD,进而可得![]() ,由余弦定理求得
,由余弦定理求得![]() 后,利用
后,利用![]() ,即可得解.
,即可得解.
(1)如图,取SB的中点H,连接AH与NH,
∵M,N分别为AD,SC的中点,∴![]() 且
且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形AHNM是平行四边形,![]() ,
,
∵![]() 平面SAB,
平面SAB,![]() 平面SAB,∴
平面SAB,∴![]() 平面SAB.
平面SAB.
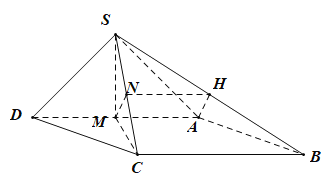
(2)设直线BN与平面SAB所成的角为![]() ,其中
,其中![]() ,点N到平面SAB的距离为d,
,点N到平面SAB的距离为d,
由(1)知![]() 平面SAB,则M到平面SAB的距离也是d,
平面SAB,则M到平面SAB的距离也是d,
∵平面![]() 平面ABCD,平面
平面ABCD,平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面SAD,又
平面SAD,又![]() 平面SAB,∴平面
平面SAB,∴平面![]() 平面SAD,
平面SAD,
又平面![]() 平面
平面![]() ,平面SAD内的直线SD垂直于两平面的交线SA,
,平面SAD内的直线SD垂直于两平面的交线SA,
∴![]() 平面SAB.
平面SAB.
∵M是等腰直角三角形ADS斜边AD的中点,所以M到平面SAB的距离d是DS的一半,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
连接SM,CM,BM,
∵平面![]() 平面ABCD,平面SAD内的直线SM垂直两平面的交线AD于点M,
平面ABCD,平面SAD内的直线SM垂直两平面的交线AD于点M,
∴![]() 平面ABCD.
平面ABCD.
由勾股定理易得![]() ,
,
∴![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴直线BN与平面SAB所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某地区城乡居民储蓄存款年底余额(单位:亿元)如图所示,下列判断一定不正确的是( )
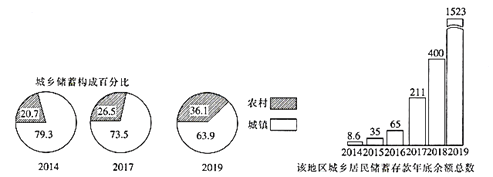
A.城乡居民储蓄存款年底余额逐年增长
B.农村居民的存款年底余额所占比重逐年上升
C.到2019年农村居民存款年底总余额已超过了城镇居民存款年底总余额
D.城镇居民存款年底余额所占的比重逐年下降
查看答案和解析>>
科目:高中数学 来源: 题型:
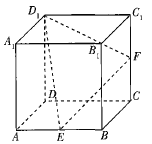
【题目】如图,在棱长为12的正方体![]() 中,已知E,F分别为棱AB,
中,已知E,F分别为棱AB,![]() 的中点,若过点
的中点,若过点![]() ,E,F的平面截正方体
,E,F的平面截正方体![]() 所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面
所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面![]() ,ABCD的交线所成角的余弦值为________.
,ABCD的交线所成角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有教师400人,其中高中教师240人.为了了解该校教师每天课外锻炼时间,现利用分层抽样的方法从该校教师中随机抽取了100名教师进行调查,统计其每天课外锻炼时间(所有教师每天课外锻炼时间均在![]() 分钟内),将统计数据按
分钟内),将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分成6组,制成频率分布直方图如下:假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
分成6组,制成频率分布直方图如下:假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
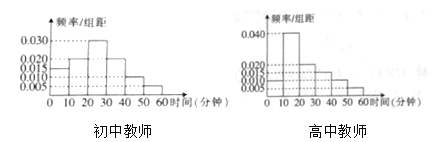
(1)试估计本校教师中缺乏锻炼的人数;
(2)从全市高中教师中随机抽取3人,若![]() 表示每天课外锻炼时间少于10分钟的人数,以这60名高中教师每天课外锻炼时间的频率代替每名高中教师每天课外锻炼时间发生的概率,求随机变量
表示每天课外锻炼时间少于10分钟的人数,以这60名高中教师每天课外锻炼时间的频率代替每名高中教师每天课外锻炼时间发生的概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】角谷猜想,也叫![]() 猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取
猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取![]() ,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若
,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若![]() ,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定下列四个命题,其中真命题是( )
A.垂直于同一直线的两条直线相互平行
B.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行
C.垂直于同一平面的两个平面相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国农历的“二十四节气”是凝结着中华民族的智慧与传统文化的结晶,“二十四节气”歌是以“春、夏、秋、冬”开始的四句诗,2016年11月30日,“二十四节气”正式被联合国教科文组织列入人类非物质文化遗产,也被誉为“中国的第五大发明”.某小学三年级共有学生500名,随机抽查100名学生并提问“二十四节气”歌,只能说出春夏两句的有45人,能说出春夏秋三句及其以上的有32人,据此估计该校三年级的500名学生中,对“二十四节气”歌只能说出第一句“春”或一句也说不出的大约有( )
A.69人B.84人C.108人D.115人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com