
【题目】角谷猜想,也叫![]() 猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取
猜想,是由日本数学家角谷静夫发现的,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2,如此循环最终都能够得到1.如:取![]() ,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若
,根据上述过程,得出6,3,10,5,16,8,4,2,1,共9个数.若![]() ,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
,根据上述过程得出的整数中,随机选取两个不同的数,则这两个数都是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为矩形,
中,底面ABCD为矩形,![]() ,
,![]() ,侧面SAD是以AD为斜边的等腰直角三角形,且平面
,侧面SAD是以AD为斜边的等腰直角三角形,且平面![]() 平面ABCD,M,N分别为AD,SC的中点.
平面ABCD,M,N分别为AD,SC的中点.
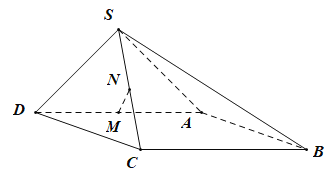
(1)求证:![]() 平面SAB.
平面SAB.
(2)求直线BN与平面SAB所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)设函数![]() (
(![]()
![]() ),讨论
),讨论![]() 的单调性;
的单调性;
(3)若对任意![]() ,恒有关于
,恒有关于![]() 的不等式
的不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 在新冠肺炎疫情的影响下,重庆市教委响应“停课不停教,停课不停学”的号召进行线上教学,某校高三年级的甲、乙两个班中,根据某次数学测试成绩各选出5名学生参加数学建模竞赛,已知这次测试他们取得的成绩的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
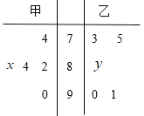
(1)求出![]() ,
,![]() 的值,且分别求甲、乙两个班中5名学生成绩的方差
的值,且分别求甲、乙两个班中5名学生成绩的方差![]() 、
、![]() ,并根据结果,你认为应该选派哪一个班的学生参加决赛,并说明你的理由.
,并根据结果,你认为应该选派哪一个班的学生参加决赛,并说明你的理由.
(2)从成绩在85分及以上的学生中随机抽取2名,用![]() 表示来自甲班的人数,求随机变量X的分布列与数学期望.
表示来自甲班的人数,求随机变量X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为4.且过点
的焦距为4.且过点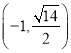 .
.
(1)求椭圆E的方程;
(2)设![]() ,
,![]() ,
,![]() ,过B点且斜率为
,过B点且斜率为![]() 的直线l交椭圆E于另一点M,交x轴于点Q,直线AM与直线
的直线l交椭圆E于另一点M,交x轴于点Q,直线AM与直线![]() 相交于点P.证明:
相交于点P.证明:![]() (O为坐标原点).
(O为坐标原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com