
【题目】如图是一“T”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m,东西向渠宽![]() m(从拐角处,即图中
m(从拐角处,即图中![]() ,
,![]() 处开始).假定渠内的水面始终保持水平位置(即无高度差).
处开始).假定渠内的水面始终保持水平位置(即无高度差).
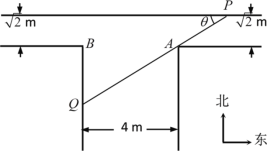
(1)在水平面内,过点![]() 的一条直线与水渠的内壁交于
的一条直线与水渠的内壁交于![]() ,
,![]() 两点,且与水渠的一边的夹角为
两点,且与水渠的一边的夹角为![]() ,将线段
,将线段![]() 的长度
的长度![]() 表示为
表示为![]() 的函数;
的函数;
(2)若从南面漂来一根长为7m的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?请说明理由.
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 过点
过点![]() 且渐近线为
且渐近线为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A.曲线![]() 的方程为
的方程为![]() ;
;
B.左焦点到一条渐近线距离为![]() ;
;
C.直线![]() 与曲线
与曲线![]() 有两个公共点;
有两个公共点;
D.过右焦点截双曲线所得弦长为![]() 的直线只有三条;
的直线只有三条;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国文明城市是中国所有城市品牌中含金量最高、创建难度最大的一个,是反映城市整体文明水平的综合性荣誉称号,是目前国内城市综合类评比中的最高荣誉,也是最具价值的城市品牌,作为普通市民,既是城市文明的最大受益者,更是文明城市的主要创造者,皖北某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取400份试卷作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
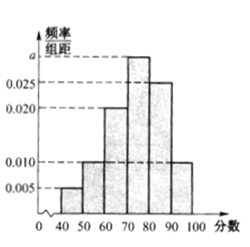
(Ⅰ)求样本的平均数;
(Ⅱ)现从该样本成绩在![]() 与
与![]() 两个分数段内的市民中按分层抽样选取6人,求从这6人中随机选取2人,且2人的竞赛成绩之差的绝对值大于20的概率.
两个分数段内的市民中按分层抽样选取6人,求从这6人中随机选取2人,且2人的竞赛成绩之差的绝对值大于20的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
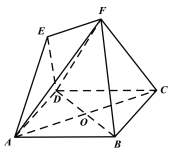
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆![]() 左、右焦点分别为
左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,两准线间距离为8,圆O的直径为
,两准线间距离为8,圆O的直径为![]() ,直线l与圆O相切于第四象限点T,与y轴交于M点,与椭圆C交于点N(N点在T点上方),且
,直线l与圆O相切于第四象限点T,与y轴交于M点,与椭圆C交于点N(N点在T点上方),且![]() .
.
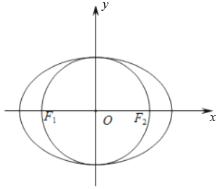
(1)求椭圆C的标准方程;
(2)求直线l的方程;
(3)求直线l上满足到![]() ,
,![]() 距离之和为
距离之和为![]() 的所有点的坐标.
的所有点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)2﹣alnx(a<0).
(1)讨论f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2(x1<x2),且关于x的方程f(x)=b(b∈R)恰有三个实数根x3,x4,x5(x3<x4<x5),求证:2(x2﹣x1)>x5﹣x3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意实数![]() 给出下列命题:①“
给出下列命题:①“![]() ”是“
”是“![]() ”的充要条件;②“
”的充要条件;②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;③“
是无理数”的充要条件;③“![]() ”是“
”是“![]() ”的充分条件;④“
”的充分条件;④“![]() ”是“
”是“![]() ”的必要条件.其中真命题的个数是( )
”的必要条件.其中真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com