
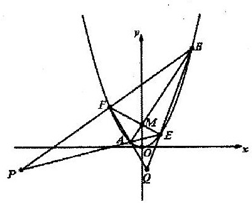
如图,过点 作抛物线
作抛物线
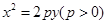 的切线
的切线 ,切点A在第二象限.
,切点A在第二象限.
(1)求切点A的纵坐标;
(2)若离心率为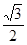 的椭圆
的椭圆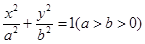 恰好经过切点A,设切线
恰好经过切点A,设切线 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线 ,OA,OB的斜率分别为
,OA,OB的斜率分别为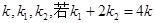 ,求椭圆方程.
,求椭圆方程.
(Ⅰ) 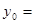
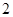 (Ⅱ)
(Ⅱ) 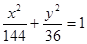
【解析】本试题主要是结合了导数的几何意义,得到直线的方程,以及运用设而不求的联立方程组的思想求解得到斜率的关系式,从而得到求解。
(1)利用导数的几何意义得到切点的横坐标,从而得到纵坐标。
(2)因为离心率为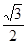 的椭圆
的椭圆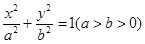 恰好经过切点A,设切线
恰好经过切点A,设切线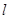 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线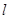 ,OA,OB的斜率分别为
,OA,OB的斜率分别为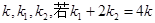 ,借助于韦达定理求解椭圆方程.
,借助于韦达定理求解椭圆方程.
解:(Ⅰ)设切点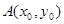 ,且
,且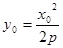 ,
,
由切线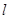 的斜率为
的斜率为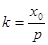 ,
,
得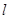 的方程为
的方程为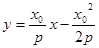 ,又点
,又点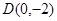 在
在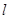 上,
上, ,即点
,即点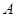 的纵坐标
的纵坐标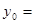
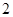 .…………5分
.…………5分
(Ⅱ)由(Ⅰ) 得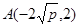 ,切线斜率
,切线斜率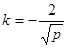 ,
,
设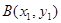 ,切线方程为
,切线方程为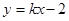 ,由
,由 ,得
,得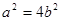 ,…………7分
,…………7分
所以椭圆方程为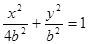 ,且过
,且过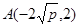 ,
,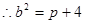 …………9分
…………9分
由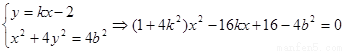 ,
,
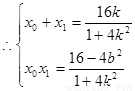 ,…………………11分
,…………………11分
∴
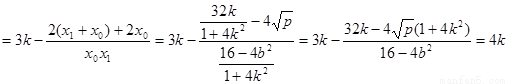
将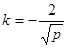 ,
,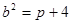 代入得:
代入得: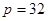 ,所以
,所以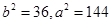 ,
,
∴椭圆方程为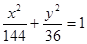 .………………13分
.………………13分
OB的斜率分别为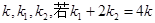 ,求椭圆方程.
,求椭圆方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 (2012•浙江模拟)己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为
(2012•浙江模拟)己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为| 17 |
| 4 |
| MP |
| MQ |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省六校高三第一次联考理科数学 题型:解答题
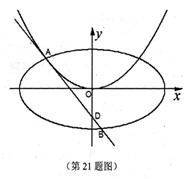
(本小题满分15分)如图,过点 作抛物线
作抛物线
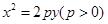 的切线
的切线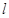 ,切点A在第二象限.
,切点A在第二象限.
(Ⅰ)求切点A的纵坐标;
(Ⅱ)若离心率为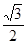 的椭圆
的椭圆 恰好经
恰好经
过切点A,设切线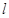 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线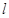 ,OA,
,OA,
OB的斜率分别为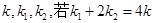 ,求椭圆方程.
,求椭圆方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分15分)
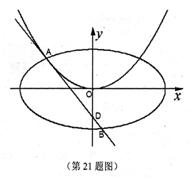
如图,过点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,切点A在第二象限,.
,切点A在第二象限,.
(Ⅰ)求切点A的纵坐标;
(Ⅱ)若离心率为![]() 的椭圆
的椭圆![]() 恰好经过切点A,设切线
恰好经过切点A,设切线![]() 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线![]() ,OA,OB的斜率分别为
,OA,OB的斜率分别为![]() ,求椭圆方程.
,求椭圆方程.
查看答案和解析>>
科目:高中数学 来源:浙江省2011-2012学年高三六校联考数学(理科)试卷 题型:解答题
如图,过点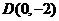 作抛物线
作抛物线
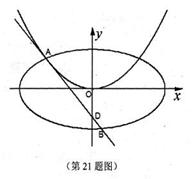
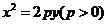 的切线
的切线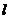 ,切点A在第二象限.
,切点A在第二象限.
(Ⅰ)求切点A的纵坐标;
(Ⅱ)若离心率为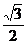 的椭圆
的椭圆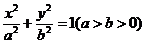 恰好经
恰好经
过切点A,设切线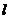 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线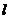 ,OA,
,OA,
OB的斜率分别为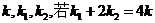 ,求椭圆方程.
,求椭圆方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com