Question

【题目】2018年4月23日“世界读书日”来临之际，某校为了了解中学生课外阅读情况，随机抽取了学生，并获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表.

组号	分组	频数	频率
1		5	0.05
2			0.35
3		30
4		20	0.20
5		10	0.10
合计		100	1

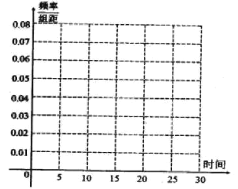
（1）求的值，并在答题卡上作出这些数据的频率分布直方图；（用阴影涂黑）

（2）根据频率分布直方图估计该组数据的众数及中位数（求中位数精确到）；

（3）现从第、、组中用分层抽样的方法抽取人参加校“中华诗词比赛”，经过比赛后从这人中选拔人组成该校代表队，求这人来自不同组别的概率.

Answer 1

【答案】（1），，频率分布直方图见解析；（2）众数为，中位数为；（3）

【解析】

（1）结合频率分布表总数为100即可求出，频数比总数可得频率即可求出的值，由此能作出频率分布直方图；

（2）由频率分布直方图最高矩形的中点值为众数，利用中位数左边矩形面积为0.5即可可求出中位数；

（3）列出基本事件总数，和满足条件的基本事件个数，用古典概型求解即可.

解：（1），

频率分布直方图如下

（2）该组数据众数的估计值为

由题图可知，中位数应在至之间，设中位数为，

则，解得，

故中位数的估计值为.

（3）易得从第、、组抽取的人数分别为、、，

第组的人设为，第组的人设为，第组的人设为，则从该人中选出人的基本事件有

共种，其中来自不同的组别的基本事件有共种，

所以这人来自不同组别的概率为.