
【题目】(本小题共13分)已知函数![]()
![]() 的最小正周期为
的最小正周期为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调区间及其图象的对称轴方程.
的单调区间及其图象的对称轴方程.
【答案】解:(Ⅰ)![]() ………………………2分
………………………2分
![]() , …………………………3分
, …………………………3分
因为![]() 最小正周期为
最小正周期为![]() ,所以
,所以![]() ,解得
,解得![]() ,………………………4分
,………………………4分
所以![]() , …………………… 5分
, …………………… 5分
所以![]() . …………………………6分
. …………………………6分
(Ⅱ)分别由![]() ,
,![]()
可得![]() ,
,![]() ………8分
………8分
所以,函数![]() 的单调增区间为
的单调增区间为![]() ;
;
![]() 的单调减区间为
的单调减区间为![]() ………………………10分
………………………10分
由![]() 得
得![]() .
.
所以,![]() 图象的对称轴方程为
图象的对称轴方程为![]() . ………………………13分
. ………………………13分
【解析】
试题(Ⅰ)![]()
![]() ,因为
,因为![]() 最小正周期为
最小正周期为![]() ,可得
,可得![]() , 可得
, 可得![]() ,即可求出
,即可求出![]() .(Ⅱ)分别由
.(Ⅱ)分别由![]() ,
,![]() 即可求出单调区间;再根据
即可求出单调区间;再根据![]() ,可得
,可得
![]() 图象的对称轴方程.
图象的对称轴方程.
试题解析:解:(Ⅰ)![]()
![]() ,
,
因为![]() 最小正周期为
最小正周期为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以![]() ,
,
所以![]() .
.
(Ⅱ)分别由![]() ,
,![]()
可得![]() ,
,![]()
所以,函数![]() 的单调增区间为
的单调增区间为![]() ;
;
![]() 的单调减区间为
的单调减区间为![]()
由![]() 得
得![]() .
.
所以,![]() 图象的对称轴方程为
图象的对称轴方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点F的坐标为
右焦点F的坐标为![]() ,点
,点![]() 在椭圆C上,过F且斜率为
在椭圆C上,过F且斜率为![]() 的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
(I)求椭圆C的方程;
(Ⅱ)设线段AB的垂直平分线与x轴、y轴分别相交于点C,D.若![]() 与
与![]() 的面积相等,求直线l的斜率k.
的面积相等,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )

A.2017年第一季度GDP增速由高到低排位第5的是浙江省
B.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
C.去年同期河南省的GDP总量不超过4000亿元
D.与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共
名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共![]() 种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以
种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以![]() 人一组或者
人一组或者![]() 人一组.如果
人一组.如果![]() 人一组,则必须角色相同;如果
人一组,则必须角色相同;如果![]() 人一组,则
人一组,则![]() 人角色相同或者
人角色相同或者![]() 人为级别连续的
人为级别连续的![]() 个不同角色.已知这
个不同角色.已知这![]() 名学生扮演的角色有
名学生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,现在新加入
人,现在新加入![]() 名学生,将这
名学生,将这![]() 名学生分成
名学生分成![]() 组进行游戏,则新加入的学生可以扮演的角色的种数为________.
组进行游戏,则新加入的学生可以扮演的角色的种数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若从第二项起的每一项均大于该项之前的所有项的和,则称
,若从第二项起的每一项均大于该项之前的所有项的和,则称![]() 为
为![]() 数列.
数列.
(1)若![]() 的前
的前![]() 项和
项和![]() ,试判断
,试判断![]() 是否是
是否是![]() 数列,并说明理由;
数列,并说明理由;
(2)设数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列,若该数列是
的等差数列,若该数列是![]() 数列,求
数列,求![]() 的取值范围;
的取值范围;
(3)设无穷数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列,有穷数列
的等比数列,有穷数列![]() ,
,![]() 是从
是从![]() 中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为
中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为![]() ,
,![]() ,求
,求![]() 是
是![]() 数列时
数列时![]() 与
与![]() 所满足的条件,并证明命题“若
所满足的条件,并证明命题“若![]() 且
且![]() ,则
,则![]() 不是
不是![]() 数列”.
数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(多选题)下列说法中,正确的命题是( )
A.已知随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() .
.
B.以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
C.已知两个变量具有线性相关关系,其回归直线方程为![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
D.若样本数据![]() ,
,![]() ,…,
,…,![]() 的方差为2,则数据
的方差为2,则数据![]() ,
,![]() ,…,
,…,![]() 的方差为16.
的方差为16.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系;曲线C1的普通方程为(x-1)2 +y2 =1,曲线C2的参数方程为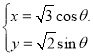 (θ为参数).
(θ为参数).
(Ⅰ)求曲线C1和C2的极坐标方程:
(Ⅱ)设射线θ=![]() (ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
(ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com