
【题目】对于数列![]() ,若从第二项起的每一项均大于该项之前的所有项的和,则称
,若从第二项起的每一项均大于该项之前的所有项的和,则称![]() 为
为![]() 数列.
数列.
(1)若![]() 的前
的前![]() 项和
项和![]() ,试判断
,试判断![]() 是否是
是否是![]() 数列,并说明理由;
数列,并说明理由;
(2)设数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列,若该数列是
的等差数列,若该数列是![]() 数列,求
数列,求![]() 的取值范围;
的取值范围;
(3)设无穷数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列,有穷数列
的等比数列,有穷数列![]() ,
,![]() 是从
是从![]() 中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为
中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为![]() ,
,![]() ,求
,求![]() 是
是![]() 数列时
数列时![]() 与
与![]() 所满足的条件,并证明命题“若
所满足的条件,并证明命题“若![]() 且
且![]() ,则
,则![]() 不是
不是![]() 数列”.
数列”.
【答案】(1)是,理由见解析;(2)![]() ;(3)当
;(3)当![]() 是
是![]() 数列时,
数列时,![]() 与
与![]() 满足的条件为
满足的条件为![]() 或
或 ,证明见解析.
,证明见解析.
【解析】
(1)由![]() 数列定义知,仅需验证当
数列定义知,仅需验证当![]() 时,
时,![]() 恒成立即可;
恒成立即可;
(2)写出![]() ,
,![]() 的表达式,则
的表达式,则![]() 对满足
对满足![]() 的任意
的任意![]() 都成立,则将此问题转化为不等式恒成立的问题,然后据此去求解
都成立,则将此问题转化为不等式恒成立的问题,然后据此去求解![]() 的范围;
的范围;
(3)根据数列![]() 是
是![]() 数列,可以得到
数列,可以得到![]() ,所以需要分
,所以需要分![]() ,
,![]() 和
和![]() ,
,![]() 去讨论,和(2)相似,还是去求解使得
去讨论,和(2)相似,还是去求解使得![]() 的
的![]() 取值范围,仍然是将其转化为不等式的恒成立问题,然后在不同的情况下求出对应的
取值范围,仍然是将其转化为不等式的恒成立问题,然后在不同的情况下求出对应的![]() 的取值范围即可.在证明命题“若
的取值范围即可.在证明命题“若![]() 且
且![]() ,则
,则![]() 不是
不是![]() 数列”时,考虑使用反证法:先排除掉数列
数列”时,考虑使用反证法:先排除掉数列![]() 的项都在数列
的项都在数列![]() 中、数列
中、数列![]() 的项都在数列
的项都在数列![]() 中的情况.若数列
中的情况.若数列![]() 至少有一项不在数列
至少有一项不在数列![]() 中,且数列
中,且数列![]() 至少有以一项不在数列
至少有以一项不在数列![]() 中,先去掉其公共项得到数列
中,先去掉其公共项得到数列![]() ,
,![]() ,设数列
,设数列![]() 的最大项为
的最大项为![]() ,且数列
,且数列![]() 的最大项比数列
的最大项比数列![]() 的最大项大,然后根据数列
的最大项大,然后根据数列![]() 是
是![]() 数列的性质,得到
数列的性质,得到![]() ,从而推出矛盾,进而所求证得证.
,从而推出矛盾,进而所求证得证.
(1)∵![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() ,
,
那么当![]() 时,
时,![]() ,符合题意,
,符合题意,
故数列![]() 是
是![]() 数列;
数列;
(2)由题意知,该数列的前![]() 项和为
项和为![]() ,
,![]() ,
,
由数列![]() 是
是![]() 数列,可知
数列,可知![]() ,故公差
,故公差![]() ,
,
![]() 对满足
对满足![]() 的任意
的任意![]() 都成立,则
都成立,则![]() ,解得
,解得![]() ,
,
故![]() 的取值范围为
的取值范围为![]() ;
;
(3)①若![]() 是
是![]() 数列,则
数列,则![]() ,
,
若![]() ,则
,则![]() ,又由
,又由![]() 对一切正整数
对一切正整数![]() 都成立,可知
都成立,可知![]() ,即
,即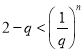 对一切正整数
对一切正整数![]() 都成立,
都成立,
由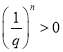 ,
,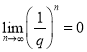 ,故
,故![]() ,可得
,可得![]() ;
;
若![]() ,则
,则![]() ,又由
,又由![]() 对一切正整数
对一切正整数![]() 都成立,可知
都成立,可知![]() ,即
,即![]() 对一切正整数
对一切正整数![]() 都成立,
都成立,
又当![]() 时,
时,![]() 当
当![]() 时不成立,
时不成立,
故有![]() 或
或![]() ,解得
,解得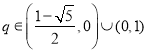 ,
,
∴当![]() 是
是![]() 数列时,
数列时,![]() 与
与![]() 满足的条件为
满足的条件为![]() 或
或 ;
;
②假设![]() 是
是![]() 数列,则由①可知,
数列,则由①可知,![]() ,
,![]() ,且
,且![]() 中每一项均为正数,
中每一项均为正数,
若![]() 中的每一项都在
中的每一项都在![]() 中,则由这两数列是不同数列,可知
中,则由这两数列是不同数列,可知![]() ;
;
若![]() 中的每一项都在
中的每一项都在![]() 中,同理可得
中,同理可得![]() ;
;
若![]() 中至少有一项不在
中至少有一项不在![]() 中且
中且![]() 中至少有一项不在
中至少有一项不在![]() 中,
中,
设![]() ,
,![]() 是将
是将![]() ,
,![]() 中的公共项去掉之和剩余项依次构成的数列,它们的所有项和分别为
中的公共项去掉之和剩余项依次构成的数列,它们的所有项和分别为![]() ,
,![]() ,
,
不妨设![]() ,
,![]() 中最大的项在
中最大的项在![]() 中,设为
中,设为![]() ,
,
则![]() ,故
,故![]() ,故总有
,故总有![]() 与
与![]() 矛盾,故假设错误,原命题正确.
矛盾,故假设错误,原命题正确.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,点E是正方体ABCD-A1B1C1D1的棱DD1的中点,点F,M分别在线段AC,BD1(不包含端点)上运动,则( )
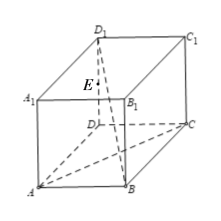
A.在点F的运动过程中,存在EF//BC1
B.在点M的运动过程中,不存在B1M⊥AE
C.四面体EMAC的体积为定值
D.四面体FA1C1B的体积不为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,M为
,M为![]() 中点,H为线段
中点,H为线段![]() 上一点(除
上一点(除![]() 的中点外),且
的中点外),且![]() .当三棱锥
.当三棱锥![]() 的体积最大时,则三棱锥
的体积最大时,则三棱锥![]() 的外接球表面积为( )
的外接球表面积为( )
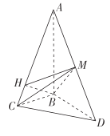
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
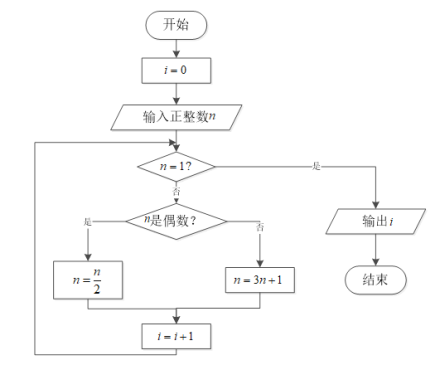
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 的焦点,点
的焦点,点![]() 为抛物线
为抛物线![]() 的对称轴与其准线的交点,过
的对称轴与其准线的交点,过![]() 作抛物线
作抛物线![]() 的切线,切点为
的切线,切点为![]() ,若点
,若点![]() 恰好在以
恰好在以![]() ,
,![]() 为焦点的双曲线上,则双曲线的离心率为( )
为焦点的双曲线上,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区为了调查高粱的高度、粒的颜色与产量的关系,对700棵高粱进行抽样调查,得到高度频数分布表如下:
表1:红粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:白粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)估计这700棵高粱中红粒高粱的棵数;画出这700棵高粱中红粒高粱的频率分布直方图;
(2)①估计这700棵高粱中高粱高(cm)在![]() 的概率;②在红粒高粱中,从高度(单位:cm)在
的概率;②在红粒高粱中,从高度(单位:cm)在![]() 中任选3棵,设
中任选3棵,设![]() 表示所选3棵中高(单位:cm)在
表示所选3棵中高(单位:cm)在![]() 的棵数,求
的棵数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com