Question

【题目】已知数列{an}的前n项和为 ．
（1）求a1 ， a2 ， a3；
（2）若数列{an}为等比数列，求常数a的值及an；
（3）对于（2）中的an ， 记f（n）=λa2n+1﹣4λan+1﹣3，若f（n）＜0对任意的正整数n恒成立，求实数λ的取值范围．

Answer 1

【答案】
（1）解：∵数列{an}的前n项和为 ，

∴a1=S1=2+a，

S2=（2+a）+a2=4+a，解得a2=2，

a3=S3﹣S2=8﹣4=4

（2）解：∵数列{an}为等比数列，

由（1）知a1=2+a，a2=2，a3=4，

∴ ，即4=（2+a）4，

解得a=﹣1．

∴ ，

∴

（3）解：∵ ，

∴f（n）=λa2n+1﹣4λan+1﹣3

=λ22n﹣4λ2n﹣3

=λ（2n﹣2）2﹣3﹣4λ＜0，

即λ[（2n﹣2）2﹣4]＜3，

分3种情况讨论：

①、λ＞0时，有λ＜ ≤﹣ ，解可得，λ＜﹣ ，此时无解；

②、λ=0时，有f（n）＜0恒成立，即λ=0符合题意；

③、λ＜0时，有λ＞ ，解可得，λ＞﹣ ，

此时λ的取值范围是﹣ ＜λ＜0；

∴综合可得：实数λ的取值范围是（﹣ ，0]

【解析】（1）利用 能求出a1 ， a2 ， a3 ． （2）由数列{an}为等比数列，得到 ，由此能求出常数a的值及an ． （3）由 ，得到f（n）=λ（2n﹣2）2﹣3﹣4λ，由此能求出结果．
【考点精析】关于本题考查的数列的前n项和和等比数列的基本性质，需要了解数列{an}的前n项和sn与通项an的关系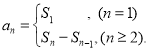；{an}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列才能得出正确答案．