练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在一个有穷数列每相邻两项之间添加一项，使其等于两相邻项的和，我们把这样的操作叫做该数列的一次“H扩展”. 已知数列1，2. 第一次“H扩展”后得到1，3，2；第二次“H扩展”后得到1，4，3，5，2； 那么第10次“H扩展”后得到的数列的所有项的和为( )

    A.88572B.88575C.29523D.29526

    【答案】B

    【解析】

    通过分析前几次中每次“扩展”后增加的项的和，得出规律：第次“扩展”后增加的项的和为，进而利用等比数列的求和公式计算即得结论．

    由题意可知，第1次“扩展”后增加的项的和为3，

    第2次“扩展”后增加的项的和为，

    第3次“扩展”后增加的项的和为，

    第次“扩展”后增加的项的和为，

    第次“扩展”后得到的数列的所有项的和为，

    于是所求值为，

    故选：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线为公海与领海的分界线，一艘巡逻艇在原点处发现了北偏东 海面上处有一艘走私船，走私船正向停泊在公海上接应的走私海轮航行，以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍，且两者都是沿直线航行，但走私船可能向任一方向逃窜.

    （1）如果走私船和巡逻船相距6海里，求走私船能被截获的点的轨迹；

    （2）若与公海的最近距离20海里，要保证在领海内捕获走私船，则，之间的最远距离是多少海里？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）讨论函数的单调性；

    （2）若，设，，若对任意，恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线，为抛物线上的点，若直线经过点且斜率为，则称直线为点的“特征直线”.设、为方程（）的两个实根，记.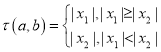

    （1）求点的“特征直线”的方程；

    （2）已知点在抛物线上，点的“特征直线”与双曲线经过二、四象限的渐进线垂直，且与轴的交于点，点为线段上的点.求证：；

    （3）已知、是抛物线上异于原点的两个不同的点，点、的“特征直线”分别为、，直线、相交于点，且与轴分别交于点、.求证：点在线段上的充要条件为（其中为点的横坐标）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱柱的底面是菱形,平面,点是侧棱上的点

    （1）证明:平面;

    （2）若是的中点,求四棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】棋盘上标有第、、、、站，棋子开始位于第站，棋手抛掷均匀硬币走跳棋游戏，若掷出正面，棋子向前跳出一站；若掷出反面，棋子向前跳出两站，直到调到第站或第站时，游戏结束.设棋子位于第站的概率为.

    （1）当游戏开始时，若抛掷均匀硬币次后，求棋手所走步数之和的分布列与数学期望；

    （2）证明：；

    （3）求、的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出定理：在圆锥曲线中，是抛物线的一条弦，是的中点，过点且平行于轴的直线与抛物线的交点为.若两点纵坐标之差的绝对值，则的面积，试运用上述定理求解以下各题：

    （1）若，所在直线的方程为，是的中点，过且平行于轴的直线与抛物线的交点为，求；

    （2）已知是抛物线的一条弦，是的中点，过点且平行于轴的直线与抛物线的交点为，分别为和的中点，过且平行于轴的直线与抛物线分别交于点，若两点纵坐标之差的绝对值，求和；

    （3）请你在上述问题的启发下，设计一种方法求抛物线：与弦围成成的“弓形”的面积，并求出相应面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业参加项目生产的工人为人，平均每人每年创造利润万元.根据现实的需要，从项目中调出人参与项目的售后服务工作，每人每年可以创造利润万元（），项目余下的工人每人每年创造利图需要提高

    （1）若要保证项目余下的工人创造的年总利润不低于原来名工人创造的年总利润，则最多调出多少人参加项目从事售后服务工作？

    （2）在（1）的条件下，当从项目调出的人数不能超过总人数的时，才能使得项目中留岗工人创造的年总利润始终不低于调出的工人所创造的年总利润，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

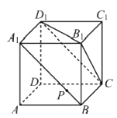
    【题目】如图，在正方体中，点在线段上移动，有下列判断：①平面平面；②平面平面；③三棱锥的体积不变；④平面．其中，正确的是______．（把所有正确的判断的序号都填上）

    查看答案和解析>>

    同步练习册答案