
【题目】平面直角坐标系xOy中,过椭圆M: ![]() (a>b>0)右焦点的直线x+y﹣
(a>b>0)右焦点的直线x+y﹣ ![]() =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为 ![]() .
.
(Ⅰ)求M的方程
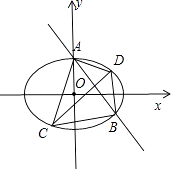
(Ⅱ)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
【答案】解:(Ⅰ)把右焦点(c,0)代入直线x+y﹣ ![]() =0得c+0﹣
=0得c+0﹣ ![]() =0,解得c=
=0,解得c= ![]() .
.
设A(x1 , y1),B(x2 , y2),线段AB的中点P(x0 , y0),
则 ![]() ,
, ![]() ,相减得
,相减得 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,又
,又 ![]() =
= ![]() ,
,
∴ ![]() ,即a2=2b2 .
,即a2=2b2 .
联立得 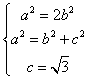 ,解得
,解得 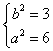 ,
,
∴M的方程为 ![]() .
.
(Ⅱ)∵CD⊥AB,∴可设直线CD的方程为y=x+t,
联立 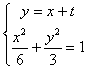 ,消去y得到3x2+4tx+2t2﹣6=0,
,消去y得到3x2+4tx+2t2﹣6=0,
∵直线CD与椭圆有两个不同的交点,
∴△=16t2﹣12(2t2﹣6)=72﹣8t2>0,解﹣3<t<3(*).
设C(x3 , y3),D(x4 , y4),∴ ![]() ,
, ![]() .
.
∴|CD|= ![]() =
= 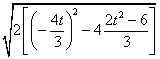 =
= ![]() .
.
联立 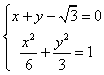 得到3x2﹣4
得到3x2﹣4 ![]() x=0,解得x=0或
x=0,解得x=0或 ![]() ,
,
∴交点为A(0, ![]() ),B
),B 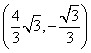 ,
,
∴|AB|= 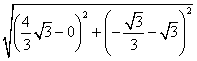 =
= ![]() .
.
∴S四边形ACBD= ![]() =
= ![]() =
= ![]() ,
,
∴当且仅当t=0时,四边形ACBD面积的最大值为 ![]() ,满足(*).
,满足(*).
∴四边形ACBD面积的最大值为 ![]() .
.
【解析】(Ⅰ)把右焦点(c,0)代入直线可解得c.设A(x1 , y1),B(x2 , y2),线段AB的中点P(x0 , y0),利用“点差法”即可得到a,b的关系式,再与a2=b2+c2联立即可得到a,b,c.(Ⅱ)由CD⊥AB,可设直线CD的方程为y=x+t,与椭圆的方程联立得到根与系数的关系,即可得到弦长|CD|.把直线x+y﹣ ![]() =0与椭圆的方程联立得到根与系数的关系,即可得到弦长|AB|,利用S四边形ACBD=
=0与椭圆的方程联立得到根与系数的关系,即可得到弦长|AB|,利用S四边形ACBD= ![]() 即可得到关于t的表达式,利用二次函数的单调性即可得到其最大值.
即可得到关于t的表达式,利用二次函数的单调性即可得到其最大值.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,动点P在底面ABCD内,且P到棱AD的距离与到面对角线BC1的距离相等,则点P的轨迹是( )
A.线段
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别是a、b、c,且满足csinA﹣ ![]() acosC=0.
acosC=0.
(1)求角C的大小;
(2)若c=2,求△ABC的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AC⊥BC,AB⊥BB1 , AC=BC=BB1 , D为AB的中点,且CD⊥DA1 . 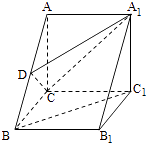
(1)求证:BC1∥平面DCA1;
(2)求BC1与平面ABB1A1所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1(﹣c,0)、F2(c,0)是椭圆 ![]() =1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1 , 则椭圆的离心率为( )
=1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1 , 则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽淮北二模】选修4—4:坐标系与参数方程
在直角坐标系![]() 中, 以
中, 以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系, 圆
轴正半轴为极轴建立极坐标系, 圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为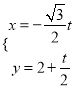 (t为参数), 直线
(t为参数), 直线![]() 和圆
和圆![]() 交于
交于![]() 两点。
两点。
(Ⅰ)求圆心的极坐标;
(Ⅱ)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一元二次不等式ax2+bx+c>0的解集是(﹣ ![]() ,2),则cx2+bx+a<0的解集是( )
,2),则cx2+bx+a<0的解集是( )
A.(﹣3, ![]() )
)
B.(﹣∞,﹣3)∪( ![]() ,+∞)
,+∞)
C.(﹣2, ![]() )
)
D.(﹣∞,﹣2)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com