已知F1(-1,0),F2(1,0),坐标平面上一点P满足:△PF1F2的周长为6,记点P的轨迹为C1.抛物线C2以F2为焦点,顶点为坐标原点O.
(Ⅰ)求C1,C2的方程;
(Ⅱ)若过F2的直线l与抛物线C2交于A,B两点,问在C1上且在直线l外是否存在一点M,使直线MA,MF2,MB的斜率依次成等差数列,若存在,请求出点M的坐标,若不存在,请说明理由.
【答案】
分析:(Ⅰ)利用△PF
1F
2的周长为6,结合椭圆的定义,可求C
1的方程;利用抛物线C
2以F
2为焦点,顶点为坐标原点O,可得C
2的方程;
(Ⅱ)设出直线方程与抛物线方程,利用直线MA,MF
2,MB的斜率依次成等差数列,即可求得结论.
解答:解:(Ⅰ)依题意可知,△PF
1F
2的周长为|PF
1|+|PF
2|+|F
1F
2|,由于|F
1F
2|=2,故|PF
1|+|PF
2|=4,
由于|PF
1|+|PF
2|>|F
1F
2|,故点P的轨迹为C
1为以F
1,F
2为焦点的椭圆的一部分,且a=2,c=1,故
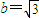
,
故C
1的方程为:
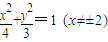
;C
2的方程为:y
2=4x.…(5分)
(Ⅱ)设A(x
1,y
1),B(x
2,y
2),M(x
,y
),设直线AB的方程为:x=my+1,
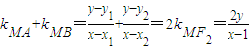
,…(6分)
故
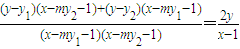
,
故
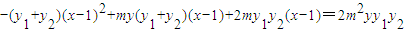
,…(8分)
由
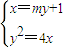
,y
2-4my-4=0,
故y
1+y
2=4m,y
1y
2=-4,…(10分)
故m(x
+1)(x
-my
-1)=0,…(11分)
因为直线AB不经过点M,故x
-my
-1≠0,故m=0或x
+1=0,…(12分)
当m=0时,C
1上除点
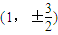
外,均符合题意;…(13分)
当m≠0时,则当x
=-1时,椭圆上存在两点
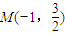
和
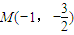
都符合条件.…(14分)
点评:本题考查椭圆、抛物线的定义,考查椭圆的定义,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

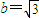 ,
,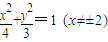 ;C2的方程为:y2=4x.…(5分)
;C2的方程为:y2=4x.…(5分)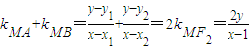 ,…(6分)
,…(6分)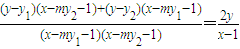 ,
,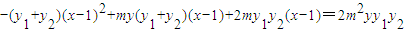 ,…(8分)
,…(8分)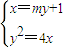 ,y2-4my-4=0,
,y2-4my-4=0,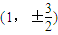 外,均符合题意;…(13分)
外,均符合题意;…(13分)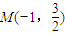 和
和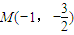 都符合条件.…(14分)
都符合条件.…(14分)
