
已知函数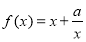 (
(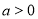 ).
).
(1)证明:当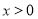 时,
时,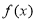 在
在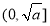 上是减函数,在
上是减函数,在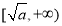 上是增函数,并写出当
上是增函数,并写出当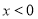 时
时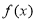 的单调区间;
的单调区间;
(2)已知函数 ,函数
,函数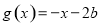 ,若对任意
,若对任意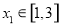 ,总存在
,总存在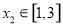 ,使得
,使得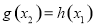 成立,求实数
成立,求实数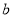 的取值范围.
的取值范围.
(1)证明详见解析,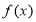 在
在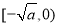 是减函数,在
是减函数,在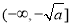 是增函数;(2)
是增函数;(2)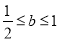 .
.
【解析】
试题分析:(1)根据函数单调性的定义进行证明即①设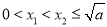 ;②作差:
;②作差: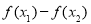 ;③因式分解到最简
;③因式分解到最简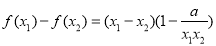 ;④根据条件判定符号;⑤作出结论,经过这五步即可证明
;④根据条件判定符号;⑤作出结论,经过这五步即可证明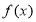 在
在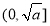 单调递减,同理可证
单调递减,同理可证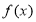 在
在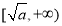 是增函数,最后由奇函数的性质得出;
是增函数,最后由奇函数的性质得出;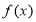 在
在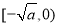 是减函数,在
是减函数,在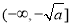 是增函数;(2)先将“对任意
是增函数;(2)先将“对任意 ,总存在
,总存在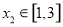 ,使得
,使得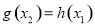 成立”转化为“函数
成立”转化为“函数 在区间
在区间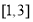 的值域包含了
的值域包含了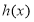 在区间
在区间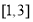 的值域”,分别根据函数的单调性求出这两个函数的值域,最后由集合的包含关系即可得到
的值域”,分别根据函数的单调性求出这两个函数的值域,最后由集合的包含关系即可得到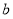 的取值范围.
的取值范围.
试题解析:(1)证明:当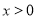 时
时
①设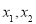 是区间
是区间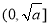 上的任意两个实数,且
上的任意两个实数,且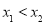 ,则
,则
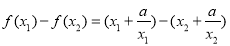
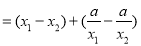

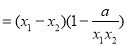
∵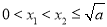 ,∴
,∴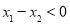 ,
,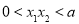
∴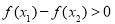 ,即
,即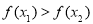
∴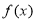 在
在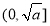 是减函数 4分
是减函数 4分
②同理可证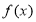 在
在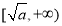 是增函数 5分
是增函数 5分
综上所述得:当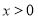 时,
时, 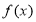 在
在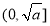 是减函数,在
是减函数,在 是增函数 6分
是增函数 6分
∵函数 是奇函数,根据奇函数图像的性质可得
是奇函数,根据奇函数图像的性质可得
当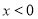 时,
时,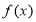 在
在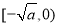 是减函数,在
是减函数,在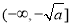 是增函数 8分
是增函数 8分
(2)∵ 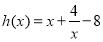 (
(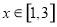 ) 8分
) 8分
由(1)知: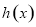 在
在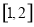 单调递减,
单调递减,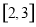 单调递增
单调递增
∴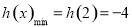
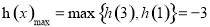 ,
,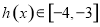 10分
10分
又∵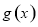 在
在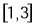 单调递减
单调递减
∴由题意知: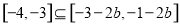
于是有: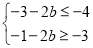 ,解得
,解得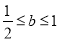 12分.
12分.
考点:1.函数的单调性与最值;2.函数的奇偶性;3.函数的值域.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:2016届河南省郑州市高一上学期期末考试数学试卷(解析版) 题型:选择题
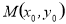 为圆
为圆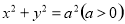 内异于圆心的一点,则直线
内异于圆心的一点,则直线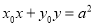 与该圆的位置关系为( )
与该圆的位置关系为( )
A. 相切 B. 相交 C. 相离 D.相切或相交
查看答案和解析>>
科目:高中数学 来源:2016届河南周口中英文学校高一下第一次月考数学试卷(解析版) 题型:选择题
已知样本数据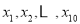 ,其中
,其中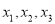 的平均数为
的平均数为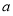 ,
,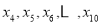 的平均数为
的平均数为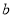 ,则样本数据的平均数为( )
,则样本数据的平均数为( )
A.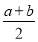 B.
B. C.
C. D.
D.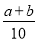
查看答案和解析>>
科目:高中数学 来源:2016届河北省邯郸市高一上学期期末考试数学试卷(解析版) 题型:选择题
已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为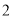 ,则该三棱锥的外接球的表面积是( )
,则该三棱锥的外接球的表面积是( )
A.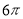 B.
B.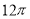 C.
C.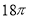 D.
D.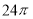
查看答案和解析>>
科目:高中数学 来源:2016届江西鹰潭市高一上学期期末考试理科数学试卷(解析版) 题型:填空题
曲线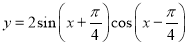 和直线
和直线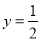 在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…,则|P2P4|等于______________。
在y轴右侧的交点按横坐标从小到大依次记为P1、P2、P3…,则|P2P4|等于______________。
查看答案和解析>>
科目:高中数学 来源:2016届江西省赣州市六校高一上学期期末联考数学试卷(解析版) 题型:填空题
函数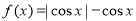 具备的性质有 . (将所有符合题意的序号都填上)
具备的性质有 . (将所有符合题意的序号都填上)
(1)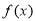 是偶函数;
是偶函数;
(2)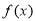 是周期函数,且最小正周期为
是周期函数,且最小正周期为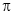 ;
;
(3)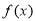 在
在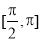 上是增加的;
上是增加的;
(4)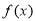 的最大值为2.
的最大值为2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com