
【题目】(导学号:05856335)[选修4-4:坐标系与参数方程]
以原点为极点,x轴的非负半轴为极轴建立极坐标系.已知A(2,π),B(2, ![]() ),圆C的极坐标方程为ρ2-6ρcos θ+8ρsin θ+21=0.F为圆C上的任意一点.
),圆C的极坐标方程为ρ2-6ρcos θ+8ρsin θ+21=0.F为圆C上的任意一点.
(Ⅰ)写出圆C的参数方程;
(Ⅱ)求△ABF的面积的最大值.
【答案】(1) ![]() (2) 9+2
(2) 9+2![]()
【解析】试题分析:(1)圆C的极坐标方程为ρ2﹣6ρcosθ+8ρsinθ+21=0,利用ρ2=x2+y2,y=ρsinθ,x=ρcosθ即可化为直角坐标方程,利用cos2α+sin2α=1可得参数方程.
(2)A(2,π),B(2, ![]() ),分别化为直角坐标:A(﹣2,0),B(0,2).可得|AB|=2
),分别化为直角坐标:A(﹣2,0),B(0,2).可得|AB|=2![]() ,直线AB的方程为:x﹣y+2=0.因此圆C上的点F到直线AB的距离取得最大值时,△ABF的面积取得最大值.
,直线AB的方程为:x﹣y+2=0.因此圆C上的点F到直线AB的距离取得最大值时,△ABF的面积取得最大值.
试题解析:
(Ⅰ)因为ρ2-6ρcos θ+8ρsin θ+21=0,故x2+y2-6x+8y+21=0,即(x-3)2+(y+4)2=4,故圆C的参数方程为![]() (θ为参数).
(θ为参数).
(Ⅱ)易知A(-2,0),B(0,2),故直线AB的方程为x-y+2=0,
点F(x,y)到直线AB:x-y+2=0的距离为d=![]() ,
,
△ABF的面积S=×|AB|×d
=|2cos θ-2sin θ+9|=|2![]() sin(
sin(![]() -θ)+9|,
-θ)+9|,
所以△ABF面积的最大值为9+2![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为![]() ,右焦点为F,上顶点为A,且△AOF的面积为
,右焦点为F,上顶点为A,且△AOF的面积为![]() (O为坐标原点).
(O为坐标原点).
(1)求椭圆C的方程;
(2)设P是椭圆C上的一点,过P的直线与以椭圆的短轴为直径的圆切于第一象限内的一点M,证明:|PF|+|PM|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像在
的图像在![]() 上连续不断,定义:
上连续不断,定义:
![]() (
(![]() ),
),![]() (
(![]() ),其中
),其中![]() 表示函数
表示函数![]() 在
在![]() 上的最小值,
上的最小值, ![]() 表示函数
表示函数![]() 在
在![]() 上的最大值,若存在最小正整数
上的最大值,若存在最小正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 成立,则称函数
成立,则称函数![]() 为
为![]() 上的“
上的“![]() 阶收缩函数”.
阶收缩函数”.
(1)若![]() ,
, ![]() ,试写出
,试写出![]() ,
, ![]() 的表达式;
的表达式;
(2)已知函数![]() ,
, ![]() ,判断
,判断![]() 是否为
是否为![]() 上的“
上的“![]() 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的![]() ,如果不是,请说明理由;
,如果不是,请说明理由;
(3)已知![]() ,函数
,函数![]() ,是
,是![]() 上的2阶收缩函数,求
上的2阶收缩函数,求![]() 的取值范围.
的取值范围.
数学附加题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856312)[选修4-5:不等式选讲]
已知函数f(x)=|x-m|-2|x-1|(m∈R).
(Ⅰ)当m=3时,求函数f(x)的最大值;
(Ⅱ)解关于x的不等式f(x)≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856330)
已知等比数列{an}的前n项和为Sn,且a3=4,a3,a4+2,a5成等差数列.数列{![]() }的前n项和为Tn.
}的前n项和为Tn.
(Ⅰ)求数列{an}的通项公式以及前n项和Sn的表达式;
(Ⅱ)若Tn<m对任意n∈N*恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
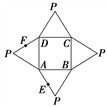
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,椭圆
,椭圆![]() 的中心在原点,
的中心在原点,![]() 为其右焦点,点
为其右焦点,点![]() 为曲线
为曲线![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为抛物线
为抛物线![]() 上的两个动点,且使得线段
上的两个动点,且使得线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
![]() 为定点,求
为定点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com