
【题目】已知函数![]() 是偶函数,
是偶函数, ![]() 是
是![]() 上的奇函数.
上的奇函数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若对![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】试题分析:(1)根据函数的奇偶性的定义求出函数解析式中的参数,特别是奇函数在x=0处有定义函数满足f(0)=0,有时利用f(0)=0也可以求参数;(2)对函数f(x)求导,根据导数的正负研究函数的单调性,进而求出函数f(x)的最小值,根据不等式恒成立的要求,利用极值原理,得出g(t)满足的要求,解不等式求出t 的取值范围.
试题解析:
(Ⅰ)∵![]() 是偶函数,∴
是偶函数,∴![]() 恒成立,
恒成立,
即![]() ,
,
∴![]() ,∴
,∴![]()
∵![]() 是
是![]() 上的奇函数,∴
上的奇函数,∴![]() ,解得
,解得![]() ,
,
此时![]() ,经检验,
,经检验, ![]() 是奇函数,
是奇函数,
∴![]() .
.
(Ⅱ)由(Ⅰ)可知![]() ,
, ![]() ,
,
当![]() 时,
时,  ,
,
∴![]() 在
在![]() 上是增函数,又因为
上是增函数,又因为![]() 是偶函数,所以
是偶函数,所以![]() 在上
在上![]() 是减函数,∴
是减函数,∴![]() ,要对
,要对![]() ,都有
,都有![]() 成立,则
成立,则![]() ,即
,即![]() ,
,
∴![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-5 不等式选讲
已知函数f(x)=|x-1|-2|x+1|的最大值为m.
(1)求m;
(2)若a,b,c∈(0,+∞),a2+2b2+c2=2m,求ab+bc的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·辽宁五校联考)某车间加工零件的数量x与加工时间y的统计数据如表:
零件数x(个) | 10 | 20 | 30 |
加工时间y(分钟) | 21 | 30 | 39 |
现已求得上表数据的线性回归方程![]() =
=![]() +
+![]() 中的
中的![]() 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A. 84分钟 B. 94分钟
C. 102分钟 D. 112分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,无穷数列
,无穷数列![]() 满足
满足![]() ,
, ![]()
(Ⅰ)若![]() ,求
,求![]() ,
, ![]() ,
, ![]() ;
;
(Ⅱ)若![]() ,且
,且![]() ,
, ![]() ,
, ![]() 成等比数列,求
成等比数列,求![]() 的值;
的值;
(Ⅲ)是否存在![]() ,使得
,使得![]() 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·成都高中毕业第一次诊断)已知双曲线![]() (a>0,b>0)的左、右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
(a>0,b>0)的左、右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
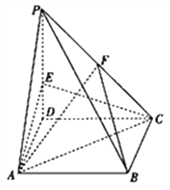
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上的一个点,
上的一个点, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
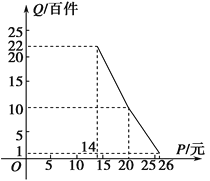
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,其中
,其中![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)已知当![]() (其中
(其中![]() 是自然对数的底数)时,在
是自然对数的底数)时,在![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,对任意
时,对任意![]() ,有
,有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com