
【题目】【2017苏北四市一模19】已知函数![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)证明:![]() ;
;
(3)是否存在常数![]() ,使得
,使得![]() 对任意的
对任意的![]() 恒成立?若存在,求
恒成立?若存在,求
出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】设直线l1 , l2分别是函数f(x)= ![]() 图象上点P1 , P2处的切线,l1与l2垂直相交于点P,且l1 , l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )
图象上点P1 , P2处的切线,l1与l2垂直相交于点P,且l1 , l2分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )
A.(0,1)
B.(0,2)
C.(0,+∞)
D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】梯形BDEF所在平面垂直于平面ABCD于BD,EF∥BD,EF=DE= ![]() BD,BD=BC=CD=
BD,BD=BC=CD= ![]() AB=
AB= ![]() AD=2,DE⊥BC.
AD=2,DE⊥BC.
(1)求证:DE⊥平面ABCD;
(2)求平面AEF与平面CEF所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,点P到两点(0,﹣![]() ),(0,
),(0,![]() )的距离之和等于4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.
)的距离之和等于4,设点P的轨迹为C,直线y=kx+1与C交于A,B两点.
(1)写出C的方程;
(2)若![]() ⊥
⊥![]() , 求k的值.
, 求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,圆C的方程为x2+y2﹣8x+15=0,若直线y=kx+2上至少存在一点,使得以该点为圆心,半径为1的圆与圆C有公共点,则k的最小值是( )
A.-![]()
B.-![]()
C.-![]()
D.-![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017徐州考前信息卷20】已知函数![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为
的最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,其中
恒成立,其中![]() 是自然对数的底数,求
是自然对数的底数,求![]() 的取值范围;
的取值范围;
(3)设曲线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,且两曲线在点
,且两曲线在点![]() 处的切线分别为
处的切线分别为![]() ,
,![]() .试判断
.试判断![]() ,
,![]() 与
与![]() 轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
轴是否能围成等腰三角形?若能,确定所围成的等腰三角形的个数;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校今年准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12,则报考飞行员的总人数是 .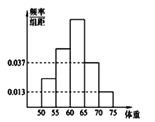
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com