练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】过抛物线 的焦点的直线与抛物线在第一象限的交点为，与抛物线准线的交点为 ，点在抛物线准线上的射影为，若 的面积为 .

    （ 1 ） 求抛物线的标准方程；

    （ 2 ） 过焦点的直线与抛物线交于两点，抛物线在点处的切线分别为，且与相交于点，与轴交于点，求证： .

    【答案】(1).

    (2)证明见解析.

    【解析】分析：（1）由题意可得，则抛物线的标准方程为.

    （2）易知直线的斜率存在，设直线，设与抛物线方程联立可得，结合切线方程可得，，则，.

    详解：（1）因为，所以到准线的距离即为三角形的中位线的长，所以，

    根据抛物线的定义，所以，

    ，

    ，

    解得，所以抛物线的标准方程为.

    （2）易知直线的斜率存在，设直线，设

    联立消去得，得，

    ，设，

    ，

    ，

    得点坐标，

    由，得，

    ,

    所以，即.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆上一点关于直线的对称点仍在圆上,直线截得圆的弦长为.

    (1)求圆的方程;

    (2)设是直线上的动点,是圆的两条切线,为切点,求四边形面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】央视传媒为了解央视举办的“朗读者”节目的收视时间情况，随机抽取了某市名观众进行调查，其中有名男观众和名女观众，将这名观众收视时间编成如图所示的茎叶图（单位：分钟），收视时间在分钟以上（包括分钟）的称为“朗读爱好者”，收视时间在分钟以下（不包括分钟）的称为“非朗读爱好者”.规定只有女“朗读爱好者”可以参加央视竞选.

    （1）若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取名，再从这名观众中任选名，求至少选到名“朗读爱好者”的概率；

    （2）若从所有的“朗读爱好者”中随机抽取名，求抽到的名观众中能参加央视竞选的人数的分布列及其数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着经济的发展，人民的收入水平逐步提高，为了解北京市居民的收入水平，某报社随机调查了名居民的月收入，得到如下的频率分布直方图：

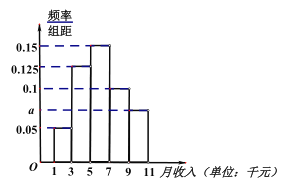
    （1）求的值及这名居民的平均月收入（同一组中的数据用该组区间的中点值作代表）

    （2）①通过大数据分析，北京人的月收入服从正态分布，其中，，求北京人收入落在的概率；

    ②将频率视为概率，若北京某公司一部门有人，记这人中月收入落在的人数为，求的数学期望.

    附：若，则

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2017湖北部分重点中学高三联考)从编号为001,002,…,500的500个产品中用系统抽样的方法抽取一个样本,已知样本编号从小到大依次为007,032,…,则样本中最大的编号应该为(　　)

    A. 483 B. 482

    C. 481 D. 480

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动点与两个定点，的距离的比为.

    （1）求动点的轨迹的方程；

    （2）过点的直线与曲线交于、两点，求线段长度的最小值；

    （3）已知圆的圆心为，且圆与轴相切，若圆与曲线有公共点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：，，，，，，后得到如图的频率分

    布直方图．

    （1）求图中实数的值；

    （2）若该校高一年级共有学生1000人，试估计该校高一年级期中考试数学成绩不低于60分的人数．

    （3）若从样本中数学成绩在，与，两个分数段内的学生中随机选取2名学生，试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018 年1月16日，由新华网和中国财经领袖联盟联合主办的2017中国财经年度人物评选结果揭晓，某知名网站财经频道为了解公众对这些年度人物是否了解，利用网络平台进行了调查，并从参与调查者中随机选出人，把这人分为 两类（类表示对这些年度人物比较了解，类表示对这些年度人物不太了解），并制成如下表格：

    年龄段

    岁～岁

    岁～岁

    岁～岁

    岁～岁

    人数

    类所占比例

    （1）若按照年龄段进行分层抽样，从这人中选出人进行访谈，并从这人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在岁～岁之间，另一名幸运者的年龄在岁～岁之间的概率；(注：从人中随机选出人,共有种不同选法)

    （2）如果把年龄在 岁～岁之间的人称为青少年，年龄在岁～岁之间的人称为中老年，则能否在犯错误的概率不超过的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异？

    参考数据：

    ，其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的多面体中, AC⊥BC,四边形ABED是正方形,平面ABED⊥平面ABC,点F,G,H分别为BD,EC,BE的中点,求证:

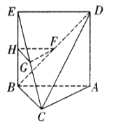
    (1) BC⊥平面ACD

    (2)平面HGF∥平面ABC.

    查看答案和解析>>

    同步练习册答案