
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)设![]() 是数列
是数列![]() 的前
的前![]() 项和,若
项和,若![]() 对任意的
对任意的![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:
(1)利用题中的递推关系计算可得后项与前项的比值为定值![]() ,计算首项为
,计算首项为![]() 即可证得数列为等比数列;
即可证得数列为等比数列;
(2)原问题转化为![]() 对任意的
对任意的![]() 都成立,分类讨论可得:实数
都成立,分类讨论可得:实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以 ,
,
又![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
(Ⅱ)由(Ⅰ)得,![]() ,即
,即![]() ,
,
则![]()
![]()
![]()
![]() .
.
又![]()
![]() ,
,
要使![]() 对任意的
对任意的![]() 都成立,
都成立,
即![]() (*)对任意的
(*)对任意的![]() 都成立.
都成立.
①当![]() 为正奇数时,由(*)得,
为正奇数时,由(*)得,![]() ,
,
即![]() ,
,
因为![]() ,
,
所以![]() 对任意的正奇数
对任意的正奇数![]() 都成立,
都成立,
当且仅当![]() 时,
时,![]() 有最小值1,
有最小值1,
所以![]() .
.
②当![]() 为正偶数时,由(*)得,
为正偶数时,由(*)得,
![]() ,
,
即![]() ,
,
因为![]() ,
,
所以![]() 对任意的正偶数
对任意的正偶数![]() 都成立.
都成立.
当且仅当![]() 时,
时,![]() 有最小值
有最小值![]() ,所以
,所以![]() .
.
综上所述,存在实数![]() ,使得
,使得![]() 对任意的
对任意的![]() 都成立,
都成立,
故实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如右表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
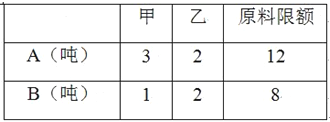
A.18万元 B.17万元 C.16万元 D.12万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD,底面ABCD是边长为2的蓌形,PA⊥平面ABCD,PA=2,∠ABC=60°,E,F分别是BC,PC的中点。
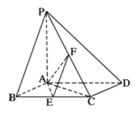
(1)求证:AE⊥PD;
(2)求二面角E-AF-C的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是我国古代数学名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“竹筒容米”就是其中一首:家有八节竹一茎,为因盛米不均平;下头三节三生九,上梢三节贮三升;唯有中间二节竹,要将米数次第盛;若是先生能算法,也教算得到天明!大意是:用一根8节长的竹子盛米,每节竹筒盛米的容积是不均匀的,下端3节可盛米3.9升,上端3节可盛米3升.要按依次盛米容积相差同一数量的方式盛米,中间两节可盛米多少升?由以上条件,计算出这根八节竹筒的容积为( )
A. ![]() 升 B.
升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
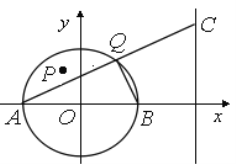
【题目】已知圆![]() ,直线
,直线![]() :x=6,圆
:x=6,圆![]() 与
与![]() 轴相交于点
轴相交于点![]() (如图),点P(-1,2)是圆
(如图),点P(-1,2)是圆![]() 内一点,点
内一点,点![]() 为圆
为圆![]() 上任一点(异于点
上任一点(异于点![]() ),直线
),直线![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)若过点P的直线![]() 与圆
与圆![]() 相交所得弦长等于
相交所得弦长等于![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在与椭圆![]() 交于
交于![]() 两点的直线
两点的直线![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】未知数的个数多余方程个数的方程(组)叫做不定方程,最早提出不定方程的是我国的《九章算术》.实际生活中有很多不定方程的例子,例如“百鸡问题”:公元五世纪末,我国古代数学家张丘建在《算经》中提出了“百鸡问题”:“鸡母一,值钱三;鸡翁一,值钱二;鸡雏二,值钱一.百钱买百鸡,问鸡翁、母、雏各几何?”
算法设计:
(1)设母鸡、公鸡、小鸡数分别为![]() 、
、![]() 、
、![]() ,则应满足如下条件:
,则应满足如下条件:
![]() ;
;![]() .
.
(2)先分析一下三个变量的可能值.①![]() 的最小值可能为零,若全部钱用来买母鸡,最多只能买33只,
的最小值可能为零,若全部钱用来买母鸡,最多只能买33只,
故![]() 的值为
的值为![]() 中的整数.②
中的整数.②![]() 的最小值为零,最大值为50.③
的最小值为零,最大值为50.③![]() 的最小值为零,最大值为100.
的最小值为零,最大值为100.
(3)对![]() 、
、![]() 、
、![]() 三个未知数来说,
三个未知数来说,![]() 取值范围最少.为提高程序的效率,先考虑对
取值范围最少.为提高程序的效率,先考虑对![]() 的值进行一一列举.
的值进行一一列举.
(4)在固定一个![]() 的值的前提下,再对
的值的前提下,再对![]() 值进行一一列举.
值进行一一列举.
(5)对于每个![]() ,
,![]() ,怎样去寻找满足百年买百鸡条件的
,怎样去寻找满足百年买百鸡条件的![]() .由于
.由于![]() ,
,![]() 值已设定,便可由下式得到:
值已设定,便可由下式得到:![]() .
.
(6)这时的![]() ,
,![]() ,
,![]() 是一组可能解,它只满足“百鸡”条件,还未满足“百钱”.是否真实解,还要看它们是否满足
是一组可能解,它只满足“百鸡”条件,还未满足“百钱”.是否真实解,还要看它们是否满足![]() ,满足即为所求解.
,满足即为所求解.
根据上述算法思想,画出流程图并用伪代码表示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com