【题目】已知函数
，其最小正周期为
.
（1）求
的表达式；
（2）将函数的图象向右平移
个单位长度后，再将得到的图象上各点的横坐标伸长到原来的
倍（纵坐标不变），得到函数
的图象，若关于
的方程
在区间
上有且只有一个实数解，求实数
的取值范围.
【答案】（1）
；（2）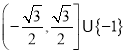
.
【解析】
（1）利用三角恒等变换思想化简函数
的解析式为
，利用函数的最小正周期可求得
的值，由此可得出函数的解析式；
（2）利用三角函数图象变换可得
，由
可计算出
的取值范围，由
可得
，可得出直线
与函数
在区间
上的图象有且只有一个交点，数形结合可求得实数
的取值范围.
（1）
，
又因为函数的最小正周期
，所以
，所以
，
所以；
（2）将函数的图象向右平移
个单位长度后，得到
的图象.再将所得图象上所有点的横坐标伸长到原来的
倍（纵坐标不变），得到
的图象，所以，
当
时，
，
令，可得，令
，可知直线与函数
在区间
上的图象有且只有一个交点，如下图所示：
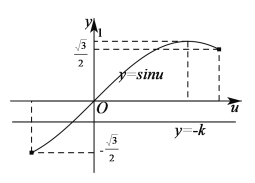
由图象可知，当
或
时，
直线与函数在区间上的图象有且只有一个交点.
所以实数的取值范围是.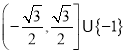
科目：高中数学 来源： 题型：
【题目】从2017年1月18日开始，支付宝用户可以通过“
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡（爱国福、富强福、和谐福、友善福，敬业福），除夕夜22:18，每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生，就除夕夜22：18之前是否集齐五福进行了一次调查（若未参与集五福的活动，则也等同于未集齐五福），得到具体数据如下表：
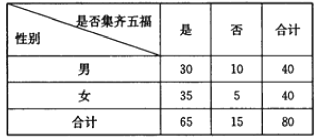
（1）根据如上的列联表，能否在犯错误的概率不超过0.05的前提下，认为“集齐五福与性别有关”？
（2）计算这80位大学生集齐五福的频率，并据此估算该校10000名在读大学生中集齐五福的人数；
（3）为了解集齐五福的大学生明年是否愿意继续参加集五福活动，该大学的学生会从集齐五福的学生中，选取2位男生和3位女生逐个进行采访，最后再随机选取3次采访记录放到该大学的官方网站上，求最后被选取的3次采访对象中至少有一位男生的概率.
参考公式：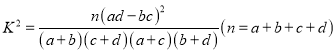 
.
附表：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近年来，共享单车已经悄然进入了广大市民的日常生活，并慢慢改变了人们的出行方式.为了更好地服务民众，某共享单车公司在其官方
中设置了用户评价反馈系统，以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
条较为详细的评价信息进行统计，车辆状况的优惠活动评价的
列联表如下：
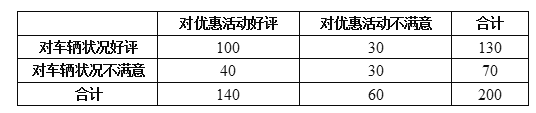
（1）能否在犯错误的概率不超过
的前提下认为优惠活动好评与车辆状况好评之间有关系？
（2）为了回馈用户，公司通过向用户随机派送骑行券.用户可以将骑行券用于骑行付费，也可以通过转赠给好友.某用户共获得了5张骑行券，其中只有2张是一元券.现该用户从这5张骑行券中随机选取2张转赠给好友，求选取的张中至少有1张是一元券的概率.
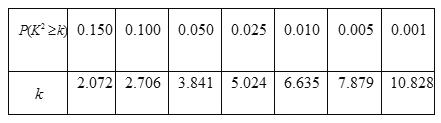
参考公式：
，其中
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业三月中旬生产A、B、C三种产品共3 000件，根据分层抽样的结果，企业统计员制作了如下的统计表格：
产品类别 | A | B | C |
产品数量（件） | 1 300 | ||
样本容量（件） | 130 |
由于不小心，表格中A、C产品的有关数据已被污染看不清楚，统计员记得A产品的样本容量比C产品的样本容量多10，根据以上信息，可得C的产品数量是（ ）
A.80B.800C.90D.900
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】△ABC的内角A，B，C所对的边分别为a，b，c.向量
＝(a，
b)与
＝(cosA，sinB)平行．
(1)求A；
(2)若a＝
，b＝2，求△ABC的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中，
，
，
所对的边分别为
，
，
，过
作直线
与边
相交于点
，
，
.当直线
时，
值为
；当为边的中点时，值为
.当，变化时，记
（即、中较大的数），则
的最小值为（ ）
A.B.C.
D.1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图半圆
的直径为4，
为直径
延长线上一点，且
，
为半圆周上任一点，以
为边作等边
（、、
按顺时针方向排列）
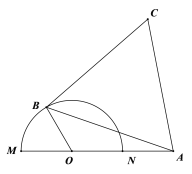
（1）若等边边长为
，
，试写出关于
的函数关系；
（2）问
为多少时，四边形
的面积最大？这个最大面积为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠BCD=135°，侧面PAB⊥底面ABCD，∠BAP=90°，AB=AC=PA=2，E、F分别为BC、AD的中点，点M在线段PD上．
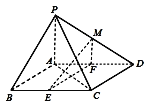
(1)求证：EF⊥平面PAC；
(2)如果直线ME与平面PBC所成的角和直线ME与平
面ABCD所成的角相等，求
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
