Question

（本小题满分12分）
已知函数其中，
（I）若求的值；（4分）         
（Ⅱ）在（I）的条件下，若函数的图像的相邻两条对称轴之间的距离等于，
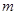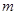①      求函数的解析式；（4分）②求最小正实数，使得函数的图象向左平移个单位时对应的函数是偶函数.（4分）

Answer 1

（I）. （Ⅱ）最小正实数。

解析试题分析：（I）利用特殊角的三角函数值化简cos cosφ-sin ，sinφ=0，根据|φ|＜ ，直接求出φ的值；
（Ⅱ）解法一：在（I）的条件下，若函数f（x）的图象的相邻两条对称轴之间的距离等于，求出周期，求出ω，得到函数f（x）的解析式；函数f（x）的图象向左平移m个单位所对应的函数是偶函数．推出m=  (k∈Z)，可求最小正实数m．
解法二：在（I）的条件下，若函数f（x）的图象的相邻两条对称轴之间的距离等于
，求出周期，求出ω，得到函数f（x）的解析式；利用g（x）是偶函数当且仅当g（-x）=g（x）对x∈R恒成立，使得函数f（x）的图象向左平移m个单位所对应的函数是偶函数．化简cos(3m+ )=0，然后再求最小正实数m．
解法一：（I）由得……2分
即又.………………4分
（Ⅱ）①由（I）得，………………5分
依题意，又.………………7分
故……………………8分
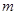②函数的图象向左平移个单位后所对应的函数为…9分
是偶函数当且仅当………………10分
即，从而，最小正实数.……………………12分
解法二：（I）同解法一………………4分
（Ⅱ）由（I）得，   依题意，
又，故………………8分
函数的图像向左平移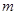个单位后所对应的函数为 
是偶函数当且仅当对恒成立……………9分
亦即对恒成立。

即对恒成立。……………………10分
故……………………11分
从而，最小正实数……………………12分
考点：本试题主要考查了三角函数的字母变量的求法，三角函数的图象的平移，偶函数的性质，转化思想的应用，考查计算能力，是常考题，中档试题。
点评：解决该试题的关键是利用两角和差的公式得到第一问的值，对于第二问，要熟练运用三角函数的性质得到。