
【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
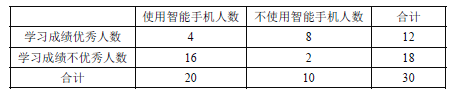
参考数据:

参考公式: 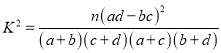 ,其中
,其中![]()
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为![]() 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为![]() 组,计划从
组,计划从![]() 组推选的2人和
组推选的2人和![]() 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自![]() 、
、![]() 两组的概率.
两组的概率.
【答案】(1)该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响;(2) ![]() .
.
【解析】试题分析:(Ⅰ)根据![]() 列联表,计算
列联表,计算![]() ,对比参考数据,
,对比参考数据, ![]() 且
且![]() ,所以有99.5%的把握认为中学生使用智能手机对学习有影响;(Ⅱ)将
,所以有99.5%的把握认为中学生使用智能手机对学习有影响;(Ⅱ)将![]() 组中的2人,和
组中的2人,和![]() 组中的3人编号,列举所有挑选两人的基本事件的个数,和其中分别来自
组中的3人编号,列举所有挑选两人的基本事件的个数,和其中分别来自![]() 两组的基本事件的个数,最后相除就是所求概率.
两组的基本事件的个数,最后相除就是所求概率.
试题解析:(Ⅰ)根据上方公式求得![]() ,
,
因为![]()
所以该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响.
(Ⅱ)记![]() 组推选的两名同学为
组推选的两名同学为![]() ,
, ![]() 组推选的三名同学为
组推选的三名同学为![]() ,
,
则从中随机选出两名同学包含如下10个基本事件:
![]()
记挑选的两人恰好分别来自![]() 两组为事件
两组为事件![]() ,
,
则事件![]() 包含如下6 个基本事件:
包含如下6 个基本事件:
![]()
故![]() .
.
即挑选的两人恰好分别来自![]() 两组的概率是
两组的概率是![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asin(x+ ![]() )﹣b(a>0)的最大值为2,最小值为0.
)﹣b(a>0)的最大值为2,最小值为0.
(1)求a、b的值;
(2)利用列表法画出函数在一个周期内的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Sn是正项数列{an}的前n项和,且Sn= ![]() an2+
an2+ ![]() an﹣
an﹣ ![]()
(1)求数列{an}的通项公式;
(2)若an=2nbn , 求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x+ ![]() )的图象,只需将y=sin2x的图象上每一个点( )
)的图象,只需将y=sin2x的图象上每一个点( )
A.横坐标向左平移 ![]() 个单位
个单位
B.横坐标向右平移 ![]() 个单位
个单位
C.横坐标向左平移 ![]() 个单位
个单位
D.横坐标向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1 . 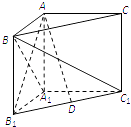
(1)求证:AB1⊥平面A1BC1;
(2)若D为B1C1的中点,求AD与平面A1BC1所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自选题:已知曲线C1: ![]() (θ为参数),曲线C2:
(θ为参数),曲线C2: 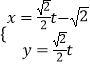 (t为参数).
(t为参数).
(1)指出C1 , C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1 , C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品每件成本为6元,每件售价为![]() 元(
元(![]() ),年销售
),年销售![]() 万件,若已知
万件,若已知![]() 与
与![]() 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润![]() 关于售价
关于售价![]() 的函数关系式.
的函数关系式.
(2)求售价为多少时,年利润最大,并求出最大年利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com