
【题目】已知圆![]() :
:![]() ,
,![]() ,
,![]() 是圆
是圆![]() 上的一个动点,线段
上的一个动点,线段![]() 的垂直平分线与线段
的垂直平分线与线段![]() 相交于点
相交于点![]() .
.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)记点![]() 的轨迹为
的轨迹为![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的两点,满足
上的两点,满足![]() ,曲线
,曲线![]() 的过
的过![]() ,
,![]() 的两条切线(异于
的两条切线(异于![]() )交于点
)交于点![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(1)由题意求出圆![]() 的圆心坐标、半径,由椭圆的定义判断出曲线
的圆心坐标、半径,由椭圆的定义判断出曲线![]() 的形状为椭圆,椭圆的标准方程即为所求;(2)直线与曲线联立,根据韦达定理,弦长公式、点到直线距离公式、三角形面积公式可得
的形状为椭圆,椭圆的标准方程即为所求;(2)直线与曲线联立,根据韦达定理,弦长公式、点到直线距离公式、三角形面积公式可得![]() 的面积,由基本不等式法求出
的面积,由基本不等式法求出![]() 面积取值范围,可得答案.
面积取值范围,可得答案.
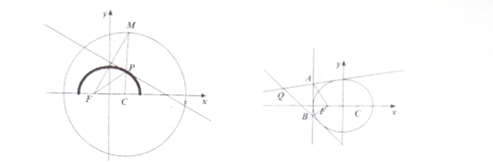
试题解析:(Ⅰ)依题意得圆心![]() ,半径
,半径![]() ,由于
,由于
![]() .
.
所以点![]() 的轨迹方程是以
的轨迹方程是以![]() ,
,![]() 为焦点,长轴长为4的椭圆,即
为焦点,长轴长为4的椭圆,即![]() ,
,![]() ,则
,则
![]() ,所以
,所以![]() 的轨迹方程是
的轨迹方程是![]() .
.
(Ⅱ)依题意,直线![]() 斜率存在且不为零,设为
斜率存在且不为零,设为![]() ,令
,令![]() 得
得![]() ,
,
同理![]() .
.
设过点![]() 的切线为
的切线为![]() ,代入
,代入![]() 得
得
![]()
![]() .
.
由![]()
![]() 解得
解得![]() ,
,
同理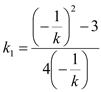
![]() .
.
联立两条切线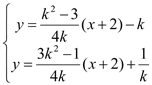 ,解得
,解得![]() .
.
![]()
![]() ,等号成立当且仅当
,等号成立当且仅当![]() ,
,
所以四边形![]() 面积的取值范围是
面积的取值范围是![]() .
.
【方法点晴】本题主要考查定义法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求四边形最值的.


科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+ ![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
(1)写出n关于x的函数关系式;
(2)写出y关于x的函数关系式;
(3)当m=640米时,需新建多少个桥墩才能使y最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在各棱长均为2的三棱柱ABC﹣A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC= ![]() ,点O为AC的中点.
,点O为AC的中点. 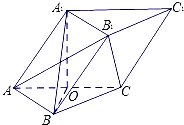
(1)求证:AC⊥平面A1OB;
(2)求二面角B1﹣AC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点所在直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() x,sin
x,sin ![]() x),
x), ![]() =(cos
=(cos ![]() x,﹣sin
x,﹣sin ![]() x),且x∈[0,
x),且x∈[0, ![]() ].求:
].求:
(1)![]() 及
及 ![]() ;
;
(2)若f(x)= ![]() ﹣2λ
﹣2λ ![]() 的最小值是﹣
的最小值是﹣ ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
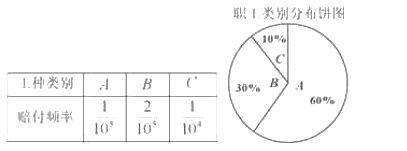
对于![]() 、
、![]() 、
、![]() 三类工种职工每人每年保费分别为
三类工种职工每人每年保费分别为![]() 元,
元,![]() 元,
元,![]() 元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(Ⅰ)若保险公司要求利润的期望不低于保费的20%,试确定保费![]() 、
、![]() 所要满足的条件;
所要满足的条件;
(Ⅱ)现有如下两个方案供企业选择;
方案1:企业不与保险公司合作,企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工;
方案2:企业于保险公司合作,企业负责职工保费的60%,职工个人负责保费的40%,出险后赔偿金由保险公司赔付.
若企业选择翻翻2的支出(不包括职工支出)低于选择方案1的支出期望,求保费![]() 、
、![]() 所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 是棱
是棱![]() 上的点,
上的点, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 体积的
体积的![]() ,设
,设![]() ,试确定
,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(2x+1)+bx+1.
(1)若函数y=f(x)在x=1处取得极值,且曲线y=f(x)在点(0,f(0))处的切线与直线2x+y﹣3=0平行,求a的值;
(2)若 ![]() ,试讨论函数y=f(x)的单调性.
,试讨论函数y=f(x)的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com