
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 在区间
在区间![]() 上是单调函数,试求
上是单调函数,试求![]() 的取值范围;
的取值范围;
(2)若函数![]() 在区间
在区间![]() 上恰有3个零点,且
上恰有3个零点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() ,再求
,再求![]() 恒成立,以及
恒成立,以及![]() 恒成立时,
恒成立时,![]() 的取值范围;
的取值范围;
(2)由已知![]() ,
,![]() 在区间
在区间![]() 内恰有一个零点,转化为
内恰有一个零点,转化为![]() 在区间
在区间![]() 内恰有两个零点,由(1)的结论对
内恰有两个零点,由(1)的结论对![]() 分类讨论,根据
分类讨论,根据![]() 单调性,结合零点存在性定理,即可求出结论.
单调性,结合零点存在性定理,即可求出结论.
(1)由题意得![]() ,则
,则![]() ,
,
当函数![]() 在区间
在区间![]() 上单调递增时,
上单调递增时,
![]() 在区间
在区间![]() 上恒成立.
上恒成立.
∴![]() (其中
(其中![]() ),解得
),解得![]() .
.
当函数![]() 在区间
在区间![]() 上单调递减时,
上单调递减时,
![]() 在区间
在区间![]() 上恒成立,
上恒成立,
∴![]() (其中
(其中![]() ),解得
),解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() .
.
由![]() ,知
,知![]() 在区间
在区间![]() 内恰有一个零点,
内恰有一个零点,
设该零点为![]() ,则
,则![]() 在区间
在区间![]() 内不单调.
内不单调.
∴![]() 在区间
在区间![]() 内存在零点
内存在零点![]() ,
,
同理![]() 在区间
在区间![]() 内存在零点
内存在零点![]() .
.
∴![]() 在区间
在区间![]() 内恰有两个零点.
内恰有两个零点.
由(1)易知,当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
故![]() 在区间
在区间![]() 内至多有一个零点,不合题意.
内至多有一个零点,不合题意.
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
故![]() 在区间
在区间![]() 内至多有一个零点,不合题意,
内至多有一个零点,不合题意,
∴![]() .令
.令![]() ,得
,得![]() ,
,
∴函数![]() 在区间
在区间![]() 上单凋递减,
上单凋递减,
在区间![]() 上单调递增.
上单调递增.
记![]() 的两个零点为
的两个零点为![]() ,
,
∴![]() ,必有
,必有![]() .
.
由![]() ,得
,得![]() .
.
∴![]()
又∵![]() ,
,
∴![]() .
.
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】为认真贯彻落实党中央国务院决策部署,坚持“房子是用来住的,不是用来炒的”定位,坚持调控政策的连续性和稳定性,进一步稳定某省市商品住房市场,该市人民政府办公厅出台了相关文件来控制房价,并取得了一定效果,下表是2019年2月至6月以来该市某城区的房价均值数据:
| 2 | 3 | 4 | 5 | 6 |
| 9.80 | 9.70 |
| 9.30 | 9.20 |
已知:![]() .
.![]()
(1)若变量![]() 、
、![]() 具有线性相关关系,求房价均价
具有线性相关关系,求房价均价![]() (千元/平方米)关于月份
(千元/平方米)关于月份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测该市某城区7月份的房价.
(参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式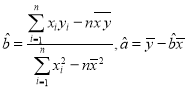 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直线![]() 将矩形纸
将矩形纸![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折的过程中(平面
翻折,如图2,在翻折的过程中(平面![]() 和平面
和平面![]() 不重合),下面说法正确的是
不重合),下面说法正确的是
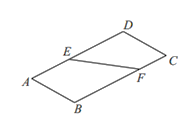
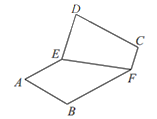
图1 图2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() ,右焦点为
,右焦点为![]() ,
,![]() 是斜率为
是斜率为![]() 的弦,
的弦,![]() 的中点为
的中点为![]() ,
,![]() 的垂直平分线交椭圆于
的垂直平分线交椭圆于![]() ,
,![]() 两点,
两点,![]() 的中点为
的中点为![]() .当
.当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() (
(![]() 为坐标原点).
为坐标原点).
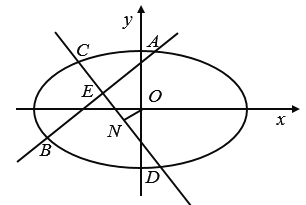
(1)求椭圆的标准方程;
(2)设原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若直线![]() ,直线
,直线![]() 的斜率满足
的斜率满足![]() ,判断并证明
,判断并证明![]() 是否为定值.
是否为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com