Question

【题目】已知椭圆的焦点坐标为，，过垂直于长轴的直线交椭圆于、两点，且.

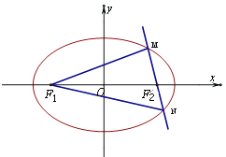
(Ⅰ)求椭圆的方程；

(Ⅱ)过的直线与椭圆交于不同的两点、，则的内切圆的面积是否存在最大值？若存在求出这个最大值及此时的直线方程；若不存在，请说明理由.

Answer 1

【答案】（1）；（2）存在，内切圆面积最大值是，直线方程为.

【解析】

(1)设椭圆方程为＝1(a>b>0)，

由焦点坐标可得c＝1.由|PQ|＝3，可得＝3.

又a2－b2＝1，得a＝2，b＝.故椭圆方程为＝1.

(2)设M(x1，y1)，N(x2，y2)，不妨令y1>0，y2<0，

设△F1MN的内切圆的半径R，

则△F1MN的周长为4a＝8，S△F1MN＝(|MN|＋|F1M|＋|F1N|)R＝4R，

因此要使△F1MN内切圆的面积最大，则R最大，此时S△F1MN也最大．

S△F1MN＝F1F2||y1－y2|＝y1－y2，

由题知，直线l的斜率不为零，可设直线l的方程为x＝my＋1，

由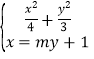得(3m2＋4)y2＋6my－9＝0，

得y1＝，y2＝，

则S△F1MN＝y1－y2＝，令t＝，则t≥1，

则S△F1MN＝＝＝.令f(t)＝3t＋，则f′(t)＝3－，

当t≥1时，f′(t)>0，所以f(t)在[1，＋∞)上单调递增，

有f(t)≥f(1)＝4，S△F1MN≤＝3，

当t＝1，m＝0时，S△F1MN＝3，又S△F1MN＝4R，∴Rmax＝

这时所求内切圆面积的最大值为π.

故△F1MN内切圆面积的最大值为π，且此时直线l的方程为x＝1.