
【题目】已知函数f(x)=sinxcos(x﹣ ![]() )+cos2x﹣
)+cos2x﹣ ![]() .
.
(1)求函数f(x)的最大值,并写出f(x)取最大值x时的取值集合;
(2)若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
【答案】
(1)解:f(x)=sinxcos(x﹣ ![]() )+cos2x﹣
)+cos2x﹣ ![]()
=sinx( ![]() cosx+
cosx+ ![]() sinx)+
sinx)+ ![]() ﹣
﹣ ![]()
= ![]() sin2x+
sin2x+ ![]() +
+ ![]() cos2x
cos2x
= ![]() sin(2x+
sin(2x+ ![]() )+
)+ ![]() ,
,
当2x+ ![]() =2kπ+
=2kπ+ ![]() (k∈Z),即x=kπ+
(k∈Z),即x=kπ+ ![]() (k∈Z)时,f(x)取得最大值
(k∈Z)时,f(x)取得最大值 ![]() .
.
函数f(x)的最大值时x的取值集合为{x|x=kπ+ ![]() (k∈Z)}
(k∈Z)}
(2)解:若f(x0)= ![]() ,即
,即 ![]() sin(2x0+
sin(2x0+ ![]() )+
)+ ![]() =
= ![]() ,
,
整理得:sin(2x0+ ![]() )=
)= ![]() ,
,
∵x0∈[ ![]() ,
, ![]() ],
],
∴2x0+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴cos(2x0+ ![]() )=﹣
)=﹣ ![]() ,
,
∴cos2x0=cos[(2x0+ ![]() )﹣
)﹣ ![]() ]=cos(2x0+
]=cos(2x0+ ![]() )cos
)cos ![]() +sin(2x0+
+sin(2x0+ ![]() )si'n
)si'n ![]() =﹣
=﹣ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]()
【解析】(1)利用两角和与差的正弦、余弦公式可化简f(x)=sinxcos(x﹣ ![]() )+cos2x﹣
)+cos2x﹣ ![]() =
= ![]() sin(2x+
sin(2x+ ![]() )+
)+ ![]() ,再利用正弦函数的性质即可求得函数f(x)的最大值及f(x)取最大值x时的取值集合;(2)x0∈[
,再利用正弦函数的性质即可求得函数f(x)的最大值及f(x)取最大值x时的取值集合;(2)x0∈[ ![]() ,
, ![]() ]2x0+
]2x0+ ![]() ∈[
∈[ ![]() ,
, ![]() ],故可求得cos(2x0+
],故可求得cos(2x0+ ![]() )=﹣
)=﹣ ![]() ,利用两角差的余弦cos2x0=cos[(2x0+
,利用两角差的余弦cos2x0=cos[(2x0+ ![]() )﹣
)﹣ ![]() ]即可求得cos2x0的值.
]即可求得cos2x0的值.


科目:高中数学 来源: 题型:
【题目】已知甲、乙两车间的月产值在2017年1月份相同,甲车间以后每个月比前一个月增加相同的产值,乙车间以后每个月比前一个月增加产值的百分比相同.到2017年7月份发现两车间的月产值又相同,比较甲、乙两个车间2017年4月份月产值的大小,则( )
A. 甲车间大于乙车间 B. 甲车间等于乙车间
C. 甲车间小于乙车间 D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设在5秒内的任何时刻,两条不相关的短信机会均等地进入同一部手机,若这两条短信进入手机的时间之差小于2秒,手机就会受到干扰,则手机受到干扰的概率为_________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂以x千克/小时的速度运输生产某种产品(生产条件要求1≤x≤10),每小时可获得利润是100(5x+1﹣ ![]() )元.
)元.
(1)写出生产该产品t(t≥0)小时可获得利润的表达式;
(2)要使生产该产品2 小时获得的利润不低于3000元,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
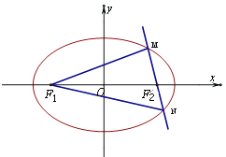
【题目】已知椭圆的焦点坐标为![]() ,
,![]() ,过
,过![]() 垂直于长轴的直线交椭圆于
垂直于长轴的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点P(1,f(1))处的切线方程为y=3x+1,y=f(x)在x=-2处有极值.
(1)求f(x)的解析式.
(2)求y=f(x)在[-3,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),已知当x∈[0,1]时,f(x)=( ![]() )1﹣x , 则
)1﹣x , 则
①2是函数f(x)的一个周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④x=1是函数f(x)的一个对称轴;
⑤当x∈(3,4)时,f(x)=( ![]() )x﹣3 .
)x﹣3 .
其中所有正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com