
【题目】如图,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,以
中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置(
的位置(![]() 平面
平面![]() ).
).
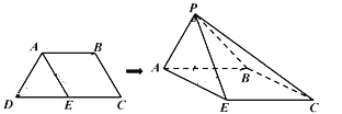
(Ⅰ)证明:![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(I)见解析;(II)![]() .
.
【解析】
(I)先证明![]() ,再证明
,再证明![]() ;(II)在平面POB内作PQ⊥OB,垂足为Q,
;(II)在平面POB内作PQ⊥OB,垂足为Q,
证明OP⊥平面ABCE,以O为原点,OE为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法求二面角![]() 的余弦值.
的余弦值.
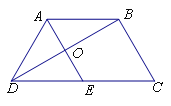
(I)证明:在等腰梯形ABCD中,连接BD,交AE于点O,
∵AB||CE,AB=CE,∴四边形ABCE为平行四边形,∴AE=BC=AD=DE,
∴△ADE为等边三角形,∴在等腰梯形ABCD中,![]() ,
,![]() ,
,
∴在等腰![]() 中,
中,![]()
∴![]() ,即BD⊥BC,
,即BD⊥BC,
∴BD⊥AE,
翻折后可得:OP⊥AE,OB⊥AE,又![]() ,
,![]() ,
,
![]() ;
;
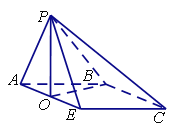
(II)解:在平面POB内作PQ⊥OB,垂足为Q,
因为AE⊥平面POB,∴AE⊥PQ,
因为OB![]() 平面ABCE, AE
平面ABCE, AE![]() 平面ABCE,AE∩OB=O
平面ABCE,AE∩OB=O
∴PQ⊥平面ABCE,∴直线PB与平面ABCE夹角为![]() ,
,
又因为OP=OB,∴OP⊥OB,
∴O、Q两点重合,即OP⊥平面ABCE,
以O为原点,OE为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,由题意得,各点坐标为![]() ,
,
设平面PCE的一个法向量为![]() ,
,
则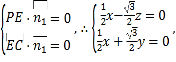
设![]() ,则y=-1,z=1,
,则y=-1,z=1,
∴![]() ,
,
由题意得平面PAE的一个法向量![]() ,
,
设二面角A-EP-C为![]() ,
,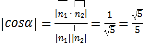 .
.
易知二面角A-EP-C为钝角,所以![]() .
.



 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,动点E到定点![]() 和定直线
和定直线![]() 的距离相等.
的距离相等.
(1)求动点E的轨迹C的方程;
(2)设动直线![]()
![]() 与曲线C有唯一的公共点P,与直线
与曲线C有唯一的公共点P,与直线![]() 相交于点Q,若
相交于点Q,若![]() ,求证:点M的轨迹恒过定点
,求证:点M的轨迹恒过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线![]()
![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“
都有公共点,则称P为“![]() 型点”.
型点”.
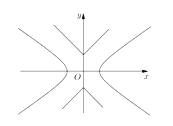
(1)若![]() ,
,![]() 时,判断
时,判断![]() 的左焦点
的左焦点![]() 是否为“
是否为“![]() 型点”,并说明理由;
型点”,并说明理由;
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“
,进而证明原点不是“![]() 型点”;
型点”;
(3)若圆![]()
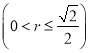 内的任意一点都不是“
内的任意一点都不是“![]() 型点”,试写出a、b满足的关系式,并说明理由.
型点”,试写出a、b满足的关系式,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】地球上的风能取之不尽,用之不竭.风能是淸洁能源,也是可再生能源.世界各国致力于发展风力发电,近10年来,全球风力发电累计装机容量连年攀升,中国更是发展迅猛,2014年累计装机容量就突破了![]() ,达到
,达到![]() ,中国的风力发电技术也日臻成熟,在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图. 根据所给信息,正确的统计结论是( )
,中国的风力发电技术也日臻成熟,在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图. 根据所给信息,正确的统计结论是( )

A.截止到2015年中国累计装机容量达到峰值
B.10年来全球新增装机容量连年攀升
C.10年来中国新增装机容量平均超过![]()
D.截止到2015年中国累计装机容量在全球累计装机容量中占比超过![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且与双曲线
,且与双曲线![]() 有相同的焦点.
有相同的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() ,点
,点![]() ,若直线
,若直线![]() 斜率为
斜率为![]() ,求
,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线
的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线![]() :
: ![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(Ⅰ)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(Ⅱ)设![]() 是坐标原点,直线
是坐标原点,直线![]() 平行于
平行于![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
(1)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)在(1)的条件下,且![]() ,求满足
,求满足![]() 的所有正整数
的所有正整数![]() ;
;
(3)若存在正整数![]() ,且
,且![]() ,试比较
,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com