Question

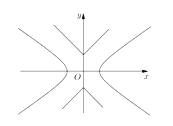
【题目】如图，已知曲线，曲线，P是平面上一点，若存在过点P的直线与都有公共点，则称P为“型点”.

（1）若，时，判断的左焦点是否为“型点”，并说明理由；

（2）设直线与有公共点，求证，进而证明原点不是“型点”；

（3）若圆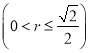内的任意一点都不是“型点”，试写出a、b满足的关系式，并说明理由.

Answer 1

【答案】（1）是，见解析；（2）见解析；（3），见解析

【解析】

（1）由双曲线方程可知，双曲线的左焦点为（，0），存在直线x分别求得交点坐标，即可说明；

（2）由直线y＝kx与C2有公共点联立方程组有实数解得到|k|＞1，分过原点的直线斜率不存在和斜率存在两种情况说明过原点的直线不可能同时与C1和C2有公共点；

（3）先考虑圆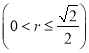内存在过Q的直线l与C1，C2都有公共点时的条件，由给出的圆的方程得到圆的图形夹在直线y＝x±1与y＝﹣x±1之间，进而说明当|k|＞1时，过圆内的点且斜率为k的直线与C2有公共点，再由圆心到直线的距离小于半径列式得出k的范围，从而得到，再取补集即可．

（1）C1的左焦点为（，0），存在直线x时，

与双曲线C1的交点为（，±），与曲线C2交点为（，±（1）），

则C1的左焦点是“C1﹣C2型点”；

（2）因为直线y＝kx与C2有公共点，

所以方程组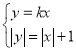有实数解，因此|kx|＝|x|+1，得|k|1．

若原点是“C1﹣C2型点”，则存在过原点的直线与C1、C2都有公共点．

考虑过原点与C2有公共点的直线x＝0或y＝kx（|k|＞1）．

显然直线x＝0与C1无公共点．

如果直线为y＝kx（|k|＞1），则由方程组，得x2，矛盾．

所以直线y＝kx（|k|＞1）与C1也无公共点．

因此原点不是“C1﹣C2型点”．

（3）记圆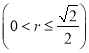，取圆O内的一点Q，

由题意圆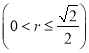内的任意一点都不是“型点”的反面是存在过Q的直线l与C1，C2都有公共点，

显然l不与x轴垂直，

故可设l：y＝kx+t．

若|k|≤1，由于圆O夹在两组平行线y＝x±1与y＝﹣x±1之间，因此圆O也夹在直线y＝kx±1与y＝﹣kx±1之间，

从而过Q且以k为斜率的直线l与C2无公共点，矛盾，所以|k|＞1．

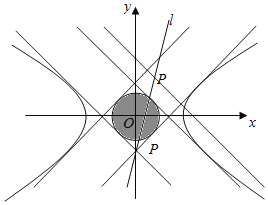
因为l与C1有公共点，所以方程组有实数解，

得（﹣k2）x2﹣ktx﹣t2﹣＝0．

因为|k|＞1，且所以﹣k2≠0，

因此△＝（kt）2﹣4（﹣k2）（﹣t2﹣）≥0，

即t2k2﹣．

因为圆O的圆心（0，0）到直线l的距离，

所以，从而k2﹣，得>k2﹣，

k2恒成立，

又k2∴当时，即时，

圆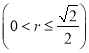内存在过Q的直线l与C1，C2都有公共点，

因此，圆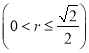内的任意一点都不是“型点”，

则需．