
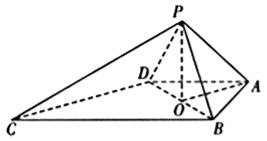
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,△
,△![]() 与△
与△![]() 都是等边三角形.
都是等边三角形.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
试题分析:(1)要证明线面垂直,就是要证线线垂直,要证![]() 与平面
与平面![]() 中两条相交直线垂直,由平面几何知识易得
中两条相交直线垂直,由平面几何知识易得![]() ,另一条垂线不易找到,考虑到
,另一条垂线不易找到,考虑到![]() ,因此
,因此![]() 在平面
在平面![]() 上的射影
上的射影![]() 是
是![]() 的外心,从而
的外心,从而![]() 是
是![]() 中点,那么可得
中点,那么可得![]() ,第二个垂直也得到了,从而证得结论;
,第二个垂直也得到了,从而证得结论;
(2)要求二面角,可根据二面角的定义先作二面角的平面角,由已知条件可得![]() ,从而
,从而![]() ,由(1)的结论可得
,由(1)的结论可得![]() ,从而又有
,从而又有![]() 平面
平面![]() ,因此
,因此![]() 就是要作的平面角,解三角形可得此角.
就是要作的平面角,解三角形可得此角.
试题解析:(1)证明:过![]() 作
作![]() 平面
平面![]() 于
于![]() ,连
,连![]() .
.
依题意![]() ,则
,则![]() .
.
又△![]() 为
为![]() ,故
,故![]() 为
为![]() 的中点.
的中点.
∵![]() 面
面![]() ,∴面
,∴面![]() 面
面![]() .
.
在梯形![]() 中,
中,![]() ,
,
∴![]() .
.
∵面![]()
![]() 面
面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,
,
又![]() ,
,
∴![]() .
.
由三垂线定理知![]() .
.
∴![]() 为二面角
为二面角![]() 的平面角,
的平面角,
∴![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】一汽车![]() 店新进
店新进![]() 三类轿车,每类轿车的数量如下表:
三类轿车,每类轿车的数量如下表:
类别 |
|
|
|
数量 | 4 | 3 | 2 |
同一类轿车完全相同,现准备提取一部分车去参加车展.
(1)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(2)若一次性提取4辆车,其中![]() 三种型号的车辆数分别记为
三种型号的车辆数分别记为![]() ,记
,记![]() 为
为![]() 的最大值,求
的最大值,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() ,若
,若![]() ,
,![]() 均是定义在实数集R上的函数,定义函数
均是定义在实数集R上的函数,定义函数![]() =
=![]() ,则下列命题正确的是( )
,则下列命题正确的是( )
A.若![]() ,
,![]() 都是单调函数,则
都是单调函数,则![]() 也是单调函数
也是单调函数
B.若![]() ,
,![]() 都是奇函数,则
都是奇函数,则![]() 也是奇函数
也是奇函数
C.若![]() ,
,![]() 都是偶函数,则
都是偶函数,则![]() 也是偶函数
也是偶函数
D.若![]() 是奇函数,
是奇函数,![]() 是偶函数,则
是偶函数,则![]() 既不是奇函数,也不是偶函数
既不是奇函数,也不是偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() ,底面
,底面![]() 是
是![]() 的菱形,侧面
的菱形,侧面![]() 是边长为
是边长为![]() 的正三角形,O是AD的中点,
的正三角形,O是AD的中点, ![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)若PO与底面ABCD垂直,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P(-1,2,3)关于xOz平面对称的点的坐标是 ( )
A. (1,2,3) B. (-1,-2,3)
C. (-1,2,-3) D. (1,-2,-3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中,正确的是( )
A.四边形是平面图形
B.有三个公共点的两个平面重合。
C.两两相交的三条直线必在同一个平面内
D.三角形必是平面图形。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)用定义证明函数![]() 在区间
在区间![]() 上为增函数;
上为增函数;
(3)若函数![]() 在区间
在区间![]() 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从学号为0~50的高一某班50名学生中随机选取5名同学参加数学测试,采用系
统抽样的方法,则所选5名学生的学号可能是:( )
A、5,15,25,35,45 B、1,2,3,4,5
C、2,4,6,8,10 D、 4,13,22,31,40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是 ( )
A. 各个面都是三角形的几何体是三棱锥
B. 以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥
C. 棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
D. 圆锥的顶点与底面圆周上的任意一点的连线都是母线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com