
【题目】如图,四棱锥![]() ,底面
,底面![]() 是
是![]() 的菱形,侧面
的菱形,侧面![]() 是边长为
是边长为![]() 的正三角形,O是AD的中点,
的正三角形,O是AD的中点, ![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)若PO与底面ABCD垂直,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(I)取AD中点 O,连接OP,OC,AC,证明OC⊥AD,OP⊥AD.推出AD⊥平面POC,即可在,PC⊥AD.(II)证明PO⊥平面ABCD.说明PO为三棱锥P-ACD的高.求出△PAC的面积,设点D到平面 PAC的距离为h,由VD-PAC=VP-ACD,求出点D到平面PAC的距离,然后求解直线DM与平面PAC所成的角的正弦值
试题解析:(1)连接![]() ,
,![]() ,
,
由题意可知![]() ,
,![]() 均为正三角形.
均为正三角形.
所以![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() .
.
(2)又![]() 平面
平面![]() .即
.即![]() 为三棱锥
为三棱锥![]() 的高.
的高.
在![]() 中,
中,![]() ,
,![]()
在![]() 中,
中,![]() ,
,![]() ,
,
边![]() 上的高
上的高![]() ,
,
所以![]() 的面积
的面积![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() 得,
得,
![]() ,
,
又![]() ,
,
所以![]() ,解得
,解得![]() .
.
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
则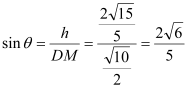 ,
,
所以直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图1,已知四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为等边三角形,
为等边三角形, ![]() ,
, ![]() ,如图2,将
,如图2,将![]() ,
, ![]() 分别沿
分别沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,设
,设![]() 为
为![]() 上任意一点.
上任意一点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:

服用B药的20位患者日平均增加的睡眠时间:

(Ⅰ)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
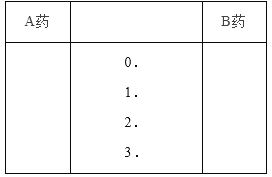
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)对一切实数x,y均有f(x+y)-f(y)=(x+2y+1)x成立,且f(1)=0.
(1)求f(0);
(2)求f(x);
(3)当0<x<2时不等式f(x)>ax-5恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com