
【题目】解关于x的不等式![]()
【答案】见解析
【解析】
根据a的范围,分a等于0和a大于0两种情况考虑:当![]() 时,把
时,把![]() 代入不等式得到一个一元一次不等式,求出不等式的解集;当a大于0时,把原不等式的左边分解因式,再根据a大于1,
代入不等式得到一个一元一次不等式,求出不等式的解集;当a大于0时,把原不等式的左边分解因式,再根据a大于1,![]() 及a大于0小于1分三种情况取解集,当a大于1时,根据
及a大于0小于1分三种情况取解集,当a大于1时,根据![]() 小于1,利用不等式取解集的方法求出解集;当
小于1,利用不等式取解集的方法求出解集;当![]() 时,根据完全平方式大于0,得到x不等于1;当a大于0小于1时,根据
时,根据完全平方式大于0,得到x不等于1;当a大于0小于1时,根据![]() 大于1,利用不等式取解集的方法即可求出解集,综上,写出a不同取值时,各自的解集即可.
大于1,利用不等式取解集的方法即可求出解集,综上,写出a不同取值时,各自的解集即可.
当![]() 时,不等式化为
时,不等式化为![]() ,
,![]() ;
;
当![]() 时,原不等式化为
时,原不等式化为![]() ,
,
![]() 当
当![]() 时,不等式的解为
时,不等式的解为![]() 或
或![]() ;
;
![]() 当
当![]() 时,不等式的解为
时,不等式的解为![]() ;
;
![]() 当
当![]() 时,不等式的解为
时,不等式的解为![]() 或
或![]() ;
;
综上所述,得原不等式的解集为:
当![]() 时,解集为
时,解集为![]() ;当
;当![]() 时,解集为
时,解集为![]() 或
或![]() ;
;
当![]() 时,解集为
时,解集为![]() ;当
;当![]() 时,解集为
时,解集为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?参考公式: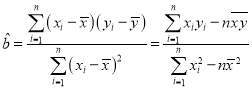 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 称为
称为![]() ,
,![]() 的二维平方平均数,
的二维平方平均数,![]() 称为
称为![]() ,
,![]() 的二维算术平均数,
的二维算术平均数,![]() 称为
称为![]() ,
,![]() 的二维几何平均数,
的二维几何平均数,![]() 称为
称为![]() ,
,![]() 的二维调和平均数,其中
的二维调和平均数,其中![]() ,
,![]() 均为正数.
均为正数.
(1)试判断![]() 与
与![]() 的大小,并证明你的猜想.
的大小,并证明你的猜想.
(2)令![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的大小,并证明你的猜想.
的大小,并证明你的猜想.
(3)令![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 、
、![]() 、
、![]() 三者之间的大小关系,并证明你的猜想.
三者之间的大小关系,并证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数集![]() ,其中
,其中![]() ,
, ![]() ,定义向量集
,定义向量集![]() .若对于任意
.若对于任意![]() ,使得
,使得![]() ,则称
,则称![]() 具有性质
具有性质![]() .例如
.例如![]() 具有性质
具有性质![]() .
.
(![]() )若
)若![]() ,且
,且![]() 具有性质
具有性质![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 具有性质
具有性质![]() ,求证:
,求证: ![]() ,且当
,且当![]() 时,
时, ![]() .
.
(![]() )若
)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() (
(![]() 为常数),求有穷数列
为常数),求有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具所需成本费用为P元,且P=1 000+5x+![]() x2,而每套售出的价格为Q元,其中Q(x)=a+
x2,而每套售出的价格为Q元,其中Q(x)=a+![]() (a,b∈R),
(a,b∈R),
(1)问:玩具厂生产多少套时,使得每套所需成本费用最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆E经过M(﹣1,0),N(0,1),P(![]() ,
,![]() )三点.
)三点.
(1)求圆E的方程;
(2)若过点C(2,2)作圆E的两条切线,切点分别是A,B,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月25日,平昌冬奥会闭幕式上的“北京8分钟”惊艳了世界。我们学校为了让我们更好的了解奥运,了解新时代祖国的科技发展,在高二年级举办了一次知识问答比赛。比赛共设三关,第一、二关各有两个问题,两个问题全答对,可进入下一关;第三关有三个问题,只要答对其中两个问题,则闯关成功。每过一关可一次性获得分别为1、2、3分的积分奖励,高二、一班对三关中每个问题回答正确的概率依次为![]() ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(1)记![]() 表示事件“高二、一班未闯到第三关”,求
表示事件“高二、一班未闯到第三关”,求![]() 的值;
的值;
(2)记![]() 表示高二、一班所获得的积分总数,求
表示高二、一班所获得的积分总数,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com