
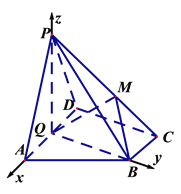
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() , 平面
, 平面![]() ,Q是AD的中点,M是棱PC上的点,
,Q是AD的中点,M是棱PC上的点,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() ;
;
(2)若平面QMB与平面PDC所成的锐二面角的大小为![]() ,求
,求![]() 的长.
的长.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】分析:(Ⅰ)先证明四边形![]() 为平行四边形,由
为平行四边形,由![]() 得
得 ![]() ,由等腰三角形的性质可得
,由等腰三角形的性质可得![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]() 平面
平面![]() ,所以
,所以 ![]() ,
,![]() ⊥平面
⊥平面![]() ,由面面垂直的判定定理可得平面
,由面面垂直的判定定理可得平面![]() ⊥平面
⊥平面![]() ;(Ⅱ)由(Ⅰ)可知
;(Ⅱ)由(Ⅰ)可知![]() 平面
平面![]() ,以
,以![]() 为原点,分别以
为原点,分别以![]() 为
为![]() 轴建立空间直角坐标系,求得平面
轴建立空间直角坐标系,求得平面![]() 法向量为
法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,利用空间向量夹角余弦公式列方程可得
,利用空间向量夹角余弦公式列方程可得![]() ,从而结果.
,从而结果.
详解:(Ⅰ)∵![]() ,
,![]() 为
为![]() 的中点,
的中点, ![]() ,∴
,∴![]()
![]() ,∴四边形
,∴四边形![]() 为平行四边形,∵
为平行四边形,∵![]() ∴
∴ ![]() .∵
.∵![]() ,∴
,∴![]() ,又∵平面
,又∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() ∩平面
∩平面![]() =
=![]() , ∴
, ∴![]() 平面
平面![]() .∴
.∴ ![]() ,又∵
,又∵![]() ,∴
,∴![]() ⊥平面
⊥平面![]() .∵
.∵![]() 平面
平面![]() ,
,
∴平面![]() ⊥平面
⊥平面![]()
(Ⅱ)由(Ⅰ)可知![]() 平面
平面![]() . 如图,以
. 如图,以![]() 为原点,分别以
为原点,分别以![]() 为
为![]() 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则![]() 由
由
![]()
![]() 又
又![]()
∴平面![]() 法向量为
法向量为![]() 由题意求
由题意求
平面![]() 的法向量为
的法向量为![]()
∵平面![]() 与
与![]() 所成的锐二面角的大小的为
所成的锐二面角的大小的为![]() ,
,
∴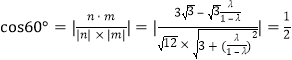 ,
,
∴![]() ∴
∴![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某工厂生产产品![]() 件的总成本
件的总成本![]() (万元).已知产品单价
(万元).已知产品单价![]() (万元)与产品件数
(万元)与产品件数![]() 满足
满足![]() ,生产100件这样的产品单价为50万元.
,生产100件这样的产品单价为50万元.
(1)设产量为![]() 件时,总利润为
件时,总利润为![]() (万元),求
(万元),求![]() 的解析式;
的解析式;
(2)产量![]() 定为多少时总利润
定为多少时总利润![]() (万元)最大?并求最大值.
(万元)最大?并求最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差为2,前n项和为Sn , 且S1 , S2 , S4成等比数列.
(1)求数列{an}的通项公式;
(2)令bn=(﹣1)n﹣1 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx)(k为常数,e=2.71828…是自然对数的底数).
+lnx)(k为常数,e=2.71828…是自然对数的底数).
(1)当k≤0时,求函数f(x)的单调区间;
(2)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
A.在区间[ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a,b,c,且a>c,已知 ![]()
![]() =2,cosB=
=2,cosB= ![]() ,b=3,求:
,b=3,求:
(1)a和c的值;
(2)cos(B﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+e﹣x , 其中e是自然对数的底数.
(1)证明:f(x)是R上的偶函数;
(2)若关于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,求实数m的取值范围;
(3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(﹣x03+3x0)成立,试比较ea﹣1与ae﹣1的大小,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com