
【题目】已知函数![]() ,
,![]() ,
,
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)欲求曲线![]() 在点
在点![]() 处的切线方程,只需求出斜率
处的切线方程,只需求出斜率![]() 和和
和和![]() 的值,即可利用直线的点斜式方程求解切线的方程;
的值,即可利用直线的点斜式方程求解切线的方程;
(2)求出![]() ,通过讨论
,通过讨论![]() 的取值范围,求出函数的单调区间,从而求出函数的极值即可,可分
的取值范围,求出函数的单调区间,从而求出函数的极值即可,可分![]() 两种情况,求出函数的单调区间,得出函数的极值.
两种情况,求出函数的单调区间,得出函数的极值.
试题解析:
(1)![]() 时,
时,![]() ,
,![]()
所以![]() ,
,![]()
因此曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]()
即![]()
(2)![]()
![]()
①当![]() 时,
时,![]() 恒成立,
恒成立,
所以当![]() 时
时![]() ,
,![]() 单调递减
单调递减
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
所以当![]() 时,
时,![]() 取极小值
取极小值![]()
②当![]() 时,由
时,由![]() 得
得![]() 或
或![]()
(ⅰ)当![]() ,即
,即![]() 时
时
由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() 时,
时,![]() 取极大值
取极大值![]() ,
,![]() 时,
时,![]() 取极小值
取极小值![]()
(ⅱ)当![]() ,即
,即![]() 时,
时,![]() 恒成立
恒成立
此时函数![]() 在
在![]() 上单调递增,函数
上单调递增,函数![]() 无极值
无极值
(ⅲ)当![]() ,即
,即![]() 时
时
由![]() 得
得![]() 或
或![]()
由![]() 得
得![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() 时,
时,![]() 取极大值
取极大值![]()
![]() 时,
时,![]() 取极小值
取极小值![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为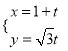 (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换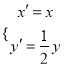 得到曲线
得到曲线![]() ,若点
,若点![]() ,直线
,直线![]() 与
与![]() 交与
交与![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
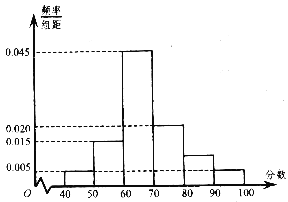
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间(满分100分,成绩不低于40分),现将成绩按如下方式分成6组:第一组![]() ;第二组
;第二组![]() ;……;第六组
;……;第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,现提供
,现提供![]() 的大致图象的8个选项:
的大致图象的8个选项:
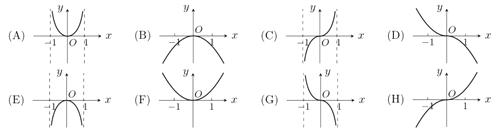
(1)请你作出选择,你选的是( );
(2)对于函数图像的判断,往往只需了解函数的基本性质.为了验证你的选择的正确性,请你解决
下列问题:
①![]() 的定义域是___________________;
的定义域是___________________;
②就奇偶性而言, ![]() 是______________________ ;
是______________________ ;
③当![]() 时,
时, ![]() 的符号为正还是负?并证明你的结论.
的符号为正还是负?并证明你的结论.
(解决了上述三个问题,你要调整你的选项,还来得及.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张师傅想要一个如图1所示的钢筋支架的组合体,来到一家钢制品加工店定制,拿出自己画的组合体三视图(如图2所示).店老板看了三视图,报了最低价,张师傅觉得很便宜,当即甩下定金和三视图,约定第二天提货.第二天提货时,店老板一脸坏笑的捧出如图3–1所示的组合体,张师傅一看,脸都绿了:“奸商,怎能如此偷工减料”.店老板说,我是按你的三视图做的,要不我给你加一个正方体,但要加价,随机加上了一个正方体,得到如图3–2所示的组合体;张师傅脸还是绿的,店老板又加上一个正方体,组成了如图 3–3 所示的组合体,又加价;张师傅脸继续绿,店老板再加一个正方体,组成如图 3–4 所示的组合体,再次加价;双方就三视图争吵不休……
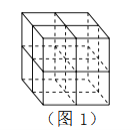
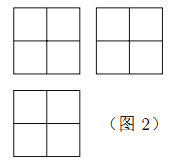
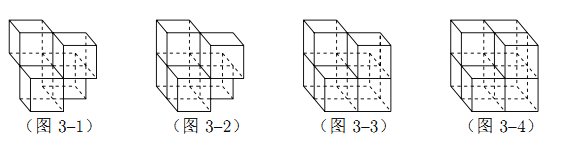
你认为店老板提供的![]() 个组合体的三视图与张师傅画的三视图一致的个数是( )
个组合体的三视图与张师傅画的三视图一致的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如下表所示:
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
根据表中信息解答以下问题:
(1)从该单位任选两名职工,求这两人休年假次数之和为4的概率;
(2)从该单位任选两名职工,用![]() 表示这两人休年假次数之差的绝对值,求随机变量
表示这两人休年假次数之差的绝对值,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() 是椭圆的焦点,直线
是椭圆的焦点,直线![]() 的斜率为
的斜率为![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上存在极值点,判断该极值点是极大值点还是极小值点,并求
上存在极值点,判断该极值点是极大值点还是极小值点,并求![]() 的取值范围;
的取值范围;
(3)若当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com