
【题目】如图,四边形![]() 是平行四边形,
是平行四边形, ![]() 平面
平面![]() ,
, ![]() ,
,
![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求多面体![]() 的体积.
的体积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算:电费每月用电不超过100度时,按每度0.57元计算;每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(Ⅰ)设月用电![]() 度时,应交电费
度时,应交电费![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用电多少度?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节7家超市的广告费支出x(万元)和销售额y(万元)数据如下,
超市 | A | B | C | D | E | F | G |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额y | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)请根据上表提供的数据.用最小二乘法求出y关于x的线性回归方程; ![]() =
= ![]() x+
x+ ![]()
(2)用二次函数回归模型拟合y与x的关系,可得回归方程: ![]() =﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
=﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
参考数据及公式: ![]() =8,
=8, ![]() =42.
=42. ![]() xiyi=2794,
xiyi=2794, ![]() x
x ![]() =708,
=708,![]() =
= 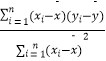 =
= 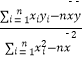 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x.
x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在各项为正的数列{an}中,数列的前n项和Sn满足Sn= ![]() (an+
(an+ ![]() ),
),
(1)求a1 , a2 , a3;
(2)由(1)猜想数列{an}的通项公式,并用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数
,那么该函数![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)用函数单调性定义来证明![]() 上的单调性;
上的单调性;
(2)已知![]() ,
, ![]() ,求函数
,求函数![]() 的值域;
的值域;
(3)对于(2)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() (a,b∈R)的图象过点P(1,f(1)),且在点P处的切线方程为y=3x﹣8.
(a,b∈R)的图象过点P(1,f(1)),且在点P处的切线方程为y=3x﹣8.
(Ⅰ)求a,b的值;
(Ⅱ)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)满足f(x﹣2)=f(x+2),且当x∈[﹣2,0]时,f(x)=3x﹣1,则f(9)=( )
A.﹣2
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的 ![]() 城市和交通拥堵严重的
城市和交通拥堵严重的 ![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):
若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此 ![]() 列联表,并据此样本分析是否有
列联表,并据此样本分析是否有 ![]() 的把握认为城市拥堵与认可共享单车有关:
的把握认为城市拥堵与认可共享单车有关:
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
附:参考数据:(参考公式: ![]() )
)
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com