分析:(Ⅰ)由b
n+2=-b
n+1-b
n,知b
3=-b
2-b
1=-3b
1=3,由此能求出b
1.
(Ⅱ)由b
n+2=-b
n+1-b
n,知b
n+3=-b
n+2-b
n+1,故b
n+3=b
n,由此能证明数列{b
nb
n+1b
n+2+n}是等差数列.
(Ⅲ)由T
n+1=T
n•b
n+1=T
n-1b
nb
n+1=T
n-2b
n-1b
nb
n+1=…=b
1b
2b
3…b
n+1,知:当n≥2时T
n=b
1b
2b
3…b
n(*),当n=1时T
1=b
1适合(*)式.故T
n=b
1b
2b
3…b
n(n∈N
*). 由
b1=-,b
2=2b
1=-1,
b3=-3b1=,b
n+3=b
n入手,能够求出求q-p的最小值.
解答:解:(Ⅰ)∵b
n+2=-b
n+1-b
n,
∴b
3=-b
2-b
1=-3b
1=3,
∴b
1=-1.(3分)
(Ⅱ)∵b
n+2=-b
n+1-b
n①
∴b
n+3=-b
n+2-b
n+1②,
②-①得b
n+3=b
n (5分)
∴(b
n+1b
n+2b
n+3+n+1)-(b
nb
n+1b
n+2+n)=b
n+1b
n+2(b
n+3-b
n)+1=1为常数
∴数列{b
nb
n+1b
n+2+n}是等差数列. (7分)
(Ⅲ)∵T
n+1=T
n•b
n+1=T
n-1b
nb
n+1=T
n-2b
n-1b
nb
n+1=…=b
1b
2b
3…b
n+1当n≥2时T
n=b
1b
2b
3…b
n(*),当n=1时T
1=b
1适合(*)式
∴T
n=b
1b
2b
3…b
n(n∈N
*). (9分)
∵
b1=-,b
2=2b
1=-1,
b3=-3b1=,b
n+3=b
n,
∴
T1=b1=-,
T2=T1b2=,
T3=T2b3=,
T4=T3b4=T3b1=T1,
T5=T4b5=T2b3b4b5=T2b1b2b3=T2,
T6=T5b6=T3b4b5b6=T3b1b2b3=T3,
…T
3n+1+T
3n+2+T
3n+3=T
3n-2b
3n-1b
3nb
3n+1+T
3n-1b
3nb
3n+1b
3n+2+T
3nb
3n+1b
3n+2b
3n+3=T
3n-2b
1b
2b
3+T
3n-1b
1b
2b
3+T
3nb
1b
2b
3=
(T3n-2+T3n-1+T3n),
∴数列
{T3n-2+T3n-1+T3n}(n∈N*)是等比数列
首项
T1+T2+T3=且公比
q= (11分)
记S
n=T
1+T
2+T
3+…+T
n①当n=3k(k∈N
*)时,S
n=(T
1+T
2+T
3)+(T
4+T
5+T
6)…+(T
3k-2+T
3k-1+T
3k)=
=
3[1-()k]∴
≤Sn<3; (13分)
②当n=3k-1(k∈N
*)时S
n=(T
1+T
2+T
3)+(T
4+T
5+T
6)…+(T
3k-2+T
3k-1+T
3k)-T
3k=
3[1-()k]-
(b1b2b3)k=
3-4•()k∴0≤S
n<3; (14分)
③当n=3k-2(k∈N
*)时S
n=(T
1+T
2+T
3)+(T
4+T
5+T
6)…+(T
3k-2+T
3k-1+T
3k)-T
3k-1-T
3k=
3[1-()k]-
(b1b2b3)k-1b1b2-
(b1b2b3)k=
3[1-()k]-
()k-1-
()k=
3-•()k∴
-≤Sn<3 (15分)
综上得
-≤Sn<3则
p≤-且q≥3,
∴q-p的最小值为
. (16分)
点评:本题考查数列中某一项的求法,等差数列的证明,探索实数是否存在.有一定的探索性,对数学思维要求较高,是高考的重点.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.



 阅读快车系列答案
阅读快车系列答案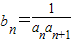 求数列{bn}的前n项和Sn.
求数列{bn}的前n项和Sn.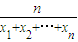 (n∈N*).已知数列{an}前n项的“倒平均数”为
(n∈N*).已知数列{an}前n项的“倒平均数”为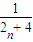 ,记cn=
,记cn= (n∈N*).
(n∈N*).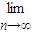 Tn.
Tn.