
(1)若直线l:y=2x+m与曲线C只有一个公共点,求实数m的取值范围;
(2)若直线l:y=kx+1与曲线C恒有两个不同的交点A和B,且![]() ·
·![]() <
<![]() (其中O为原点),求实数k的取值范围.
(其中O为原点),求实数k的取值范围.
解:(1)曲线为双曲线4x2-y2=1的上半部分(含与x轴交点)和椭圆4x2+y2=1的下半部分构成,图象如图所示,
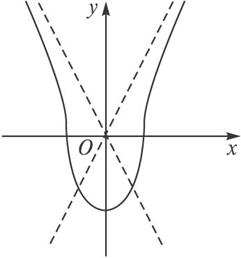
双曲线渐近线为y=±2x,直线y=2x+m与双曲线的一条渐近线平行?,
联立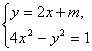 得4mx+m2+1=0,可得m≠0时,直线与完整的双曲线只能有一个交点;
得4mx+m2+1=0,可得m≠0时,直线与完整的双曲线只能有一个交点;
联立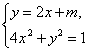 得8x2+4mx+m2-1=0,由Δ=0解得m=-2时直线与椭圆下半部分相切;
得8x2+4mx+m2-1=0,由Δ=0解得m=-2时直线与椭圆下半部分相切;
综上可得:当m≥1时,直线与双曲线有一个交点;当0≤m<1时,直线只与椭圆有一个交点;
当-1<m<0时,直线与双曲线和椭圆各有一个交点;当-![]() <m≤-1时,直线与椭圆有两个交点;
<m≤-1时,直线与椭圆有两个交点;
当m=-![]() 时,直线只与椭圆有一个交点.所以实数m的取值范围为m=-
时,直线只与椭圆有一个交点.所以实数m的取值范围为m=-![]() 或m≥0.
或m≥0.
(2)直线l:y=kx+1与曲线C恒有两个不同的交点A和B,由题可得只能交双曲线上半部分于A和B两点.
联立l:y=kx+1与4x2-y2=1可得(4-k2)x2-2kx-2=0,设A(x1,y1),B(x2,y2),由题可得-2<k<2,
又y1y2=k2x1x2+k(x1+x2)+1=1,由![]() ·
·![]() <
<![]() 可得x1x2+y1y2<
可得x1x2+y1y2<![]() ,解得k2>1,所以-2<k<-1或1<k<2.
,解得k2>1,所以-2<k<-1或1<k<2.


科目:高中数学 来源: 题型:
| OA |
| OB |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:河北省衡水中学2011-2012学年高二上学期四调考试数学理科试题 题型:044
已知曲线C:4x2-y|y|=1
(Ⅰ)若直线l:y=2x+m与曲线C只有一个公共点,求实数m的取值范围;
(Ⅱ)若直线l:y=kx+1与曲线C恒有两个不同的交点A和B,且![]() ·
·![]() <
<![]() (其中O为坐标原点),求实数k的取值范围.
(其中O为坐标原点),求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:福建省福州三中2012届高三第四次月考数学理科试题 题型:044
已知曲线C:4x2+12xy+9y2-6x-3y=0在矩阵![]() 所对应的变换作用下得到曲线C1,求曲线C1的方程及焦点到准线的距离.
所对应的变换作用下得到曲线C1,求曲线C1的方程及焦点到准线的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若直线l:y=2x+m与曲线C只有一个公共点,求实数m的取值范围;
(2)若直线l:y=kx+1与曲线C恒有两个不同的交点A和B,且![]() ·
·![]() <
<![]() (其中O为原点),求实数k的取值范围.
(其中O为原点),求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com