练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    椭圆+ =1的右焦点为F,过点A(1,3),点M在椭圆上,当|AM|+2|MF|为最小值时,求点M的坐标.

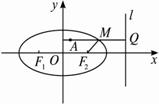
    思路分析:关键是对于|AM|+2|MF|中的“2”的处理,把2|MF|转化为M到右准线的距离,从而得到最小值.一般地,求|AM|+|MF|均可用此法.?

    解析:由已知a=4,c=2,得e=,右准线l:x=8.?

    过A作AQ⊥l,垂足为Q,交椭圆于M.故|MQ|=2|MF|,显然|AM|+2|MF|的最小值为|AQ|,即M为所求点.因此,ym=且M点在椭圆上,故xm=2.

    ∴M(2,).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知斜率为1的直线l经过椭圆+y2=1的右焦点交椭圆于A、B两点,则弦AB的长是__________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    以椭圆+y2=1的右焦点F为焦点,以坐标原点为顶点作抛物线,抛物线与椭圆的一个公共点是A,则|AF|等于（    ）

    A.9+22         B.9-185           C.9-20            D.9-22

    查看答案和解析>>

    科目：高中数学 来源：2012－2013学年江西省高二第一次月考文科数学试卷（解析版） 题型：填空题

    已知点A(4,4)，若抛物线y2＝2px的焦点与椭圆＝1的右焦点重合，该抛物线上有一点M，它在y轴上的射影为N，则|MA|＋|MN|的最小值为___________

     

    查看答案和解析>>

    科目：高中数学 来源：2013届湖南省华容县高二第一学期期末考试理科数学试卷 题型：填空题

    已知点A(4,4)，若抛物线y2＝2px的焦点与椭圆＝1的右焦点重合，该抛物线上有一点M，它在y轴上的射影为N，则|MA|＋|MN|的最小值为___________。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设F为椭圆+y2=1的右焦点,O为坐标原点,P为坐标平面上一动点,且·=t(t＞-1且t为常数).

    (1)求点P的轨迹方程.

    (2)当t=时,是否存在直线l,使l是椭圆与(1)中轨迹的公切线?若存在,求出l的方程;若不存在,请说明理由.

    查看答案和解析>>

    同步练习册答案