
【题目】已知曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),直线
为参数),直线 ![]() 的参数方程为
的参数方程为  (
( ![]() 为参数).
为参数).
(Ⅰ)求曲线 ![]() 和直线
和直线 ![]() 的普通方程;
的普通方程;
(Ⅱ)若点 ![]() 为曲线
为曲线 ![]() 上一点,求点
上一点,求点 ![]() 到直线
到直线 ![]() 的距离的最大值.
的距离的最大值.
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=3x-x3在区间(a2-12,a)上有最小值,则实数a的取值范围是( )
A.(-1,3)
B.(-1,2)
C.(-1,3]
D.(-1,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区 ![]() 的年平均浓度不得超过3S微克/立方米,
的年平均浓度不得超过3S微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天
的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天 ![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
组别 |
| 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
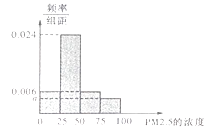
(Ⅰ)将这20天的测量结果按表中分组方法绘制成的样本频率分布直方图如图.
(ⅰ)求图中 ![]() 的值;
的值;
(ⅱ)在频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从 ![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(Ⅱ)将频率视为概率,对于2016年的某3天,记这3天中该居民区 ![]() 的24小时平均浓度符合环境空气质量标准的天数为
的24小时平均浓度符合环境空气质量标准的天数为 ![]() ,求
,求 ![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为
的最小正周期为 ![]() ,将函数
,将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位长度,再向下平移
个单位长度,再向下平移 ![]() 个单位长度,得到函数
个单位长度,得到函数 ![]() 的图象.
的图象.
(Ⅰ)求函数 ![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)在锐角 ![]() 中,角
中,角 ![]() 的对边分别为
的对边分别为 ![]() .若
.若 ![]() ,
, ![]() ,求
,求 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (
( ![]() )在同一半周期内的图象过点
)在同一半周期内的图象过点 ![]() ,
, ![]() ,
, ![]() ,其中
,其中 ![]() 为坐标原点,
为坐标原点, ![]() 为函数
为函数 ![]() 图象的最高点,
图象的最高点, ![]() 为函数
为函数 ![]() 的图象与
的图象与 ![]() 轴的正半轴的交点,
轴的正半轴的交点, ![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求 ![]() 的值;
的值;
(2)将 ![]() 绕原点
绕原点 ![]() 按逆时针方向旋转角
按逆时针方向旋转角 ![]() ,得到
,得到 ![]() ,若点
,若点 ![]() 恰好落在曲线
恰好落在曲线 ![]() (
( ![]() )上(如图所示),试判断点
)上(如图所示),试判断点 ![]() 是否也落在曲线
是否也落在曲线 ![]() (
( ![]() )上,并说明理由.
)上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形 ![]() 中,点
中,点 ![]() 在线段
在线段 ![]() 上,
上, ![]() ,
, ![]() ,沿直线
,沿直线 ![]() 将
将 ![]() 翻折成
翻折成 ![]() ,使点
,使点 ![]() 在平面
在平面 ![]() 上的射影
上的射影 ![]() 落在直线
落在直线 ![]() 上.
上.
(Ⅰ)求证:直线 ![]() 平面
平面 ![]() ;
;
(Ⅱ)求二面角 ![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:①已知 ![]() ,“
,“ ![]() 且
且 ![]() ”是“
”是“ ![]() ”的充分条件;
”的充分条件;
②已知平面向量 ![]() ,
, ![]() 是“
是“ ![]() ”的必要不充分条件;
”的必要不充分条件;
③已知 ![]() ,“
,“ ![]() ”是“
”是“ ![]() ”的充分不必要条件;
”的充分不必要条件;
④命题 ![]() “
“ ![]() ,使
,使 ![]() 且
且 ![]() ”的否定为
”的否定为 ![]() “
“ ![]() ,都有
,都有 ![]() 且
且 ![]() ”.其中正确命题的个数是( )
”.其中正确命题的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com