
【题目】如图,在平面四边形ABCD中,已知∠A= ![]() ,∠B=
,∠B= ![]() ,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=
,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED= ![]() ,EC=
,EC= ![]() .
. 
(Ⅰ)求sin∠BCE的值;
(Ⅱ)求CD的长.
【答案】解:(Ⅰ)在△CBE中,由正弦定理得 ![]() ,sin∠BCE=
,sin∠BCE= 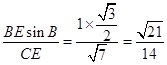 , (Ⅱ)在△CBE中,由余弦定理得CE2=BE2+CB2﹣2BECBcos120°,即7=1+CB2+CB,解得CB=2.
, (Ⅱ)在△CBE中,由余弦定理得CE2=BE2+CB2﹣2BECBcos120°,即7=1+CB2+CB,解得CB=2.
由余弦定理得CB2=BE2+CE2﹣2BECEcos∠BECcos∠BEC= ![]() .sin∠BEC=
.sin∠BEC= ![]() ,
,
sin∠AED=sin(1200+∠BEC)= ![]() ,cos∠AED=
,cos∠AED= ![]() ,
,
在直角△ADE中,AE=5, ![]() ═cos∠AED=
═cos∠AED= ![]() ,DE=2
,DE=2 ![]() ,
,
在△CED中,由余弦定理得CD2=CE2+DE2﹣2CEDEcos120°=49
∴CD=7.
【解析】(Ⅰ)在△CBE中,正弦定理求出sin∠BCE;(Ⅱ)在△CBE中,由余弦定理得CE2=BE2+CB2﹣2BECBcos120°,得CB.由余弦定理得CB2=BE2+CE2﹣2BECEcos∠BECcos∠BECsin∠BEC、cos∠AED在直角△ADE中,求得DE=2 ![]() ,在△CED中,由余弦定理得CD2=CE2+DE2﹣2CEDEcos120°即可
,在△CED中,由余弦定理得CD2=CE2+DE2﹣2CEDEcos120°即可


科目:高中数学 来源: 题型:
【题目】某工厂拟生产甲、乙两种实销产品.已知每件甲产品的利润为0.4万元,每件乙产品的利润为0.3万元,两种产品都需要在A,B两种设备上加工,且加工一件甲、乙产品在A,B设备上所需工时(单位:h)分别如表所示.
甲产品所需工时 | 乙产品所需工时 | |
A设备 | 2 | 3 |
B设备 | 4 | 1 |
若A设备每月的工时限额为400h,B设备每月的工时限额为300h,则该厂每月生产甲、乙两种产品可获得的最大利润为( )
A.40万元
B.45万元
C.50万元
D.55万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,2acosC=bcosC+ccosB.
(1)求角C的大小;
(2)若c=![]() ,a2+b2=10,求△ABC的面积.
,a2+b2=10,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足:Sn=nan﹣2n(n﹣1),首项![]() =1.
=1.
(1)求数列{an}的通项公式;
(2)设数列![]() 的前n项和为Mn,求证:
的前n项和为Mn,求证:![]()
![]() Mn
Mn![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为双曲线
分别为双曲线![]() 的左、右顶点,双曲线的实轴长为
的左、右顶点,双曲线的实轴长为![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为![]() .
.
(1)求双曲线的方程;
(2)已知直线![]() 与双曲线的右支交于
与双曲线的右支交于![]() 两点,且在双曲线的右支上存在点
两点,且在双曲线的右支上存在点![]() ,使
,使![]() ,求
,求![]() 的值及点
的值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (t为参数).直线
(t为参数).直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx+cosωx(ω>0),x∈R,若函数f(x)在区间(﹣ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() ,
,![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.

(1)求证:![]() ;
;
(2)若![]() 为
为![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】泰兴机械厂生产一种木材旋切机械,已知生产总利润c元与生产量x台之间的关系式为c(x)=-2x2+7 000x+600.
(1)求产量为1 000台的总利润与平均利润;
(2)求产量由1 000台提高到1 500台时,总利润的平均改变量;
(3)求c′(1 000)与c′(1 500),并说明它们的实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com