
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() ,
,![]() 交于点
交于点![]() ,
,![]() 是
是![]() 上任意一点.
上任意一点.

(1)求证:![]() ;
;
(2)若![]() 为
为![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)先求证AC⊥平面PBD,再证AC⊥DE.(2)先证明 EO⊥平面ABCD,分别以OA,OB,OE所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,再利用向量法求出EC与平面PAB所成角![]() 的正弦值.
的正弦值.
(1)因为DP⊥平面ABCD,所以DP⊥AC,
因为四边形ABCD为菱形,所以BD⊥AC,
又BD∩PD=D,∴AC⊥平面PBD,
因为DE平面PBD,∴AC⊥DE.
(2)连接OE,在△PBD中,EO∥PD,
所以EO⊥平面ABCD,分别以OA,OB,OE所在直线为x轴,y轴,z轴,
建立如图所示的空间直角坐标系,
设PD=t,则A(1,0,0),B(0,![]() ,0),C(﹣1,0,0),
,0),C(﹣1,0,0),
E(0,0,![]() ),P(0,﹣
),P(0,﹣![]() ,t).
,t).
设平面PAB的一个法向量为![]() (x,y,z),
(x,y,z),
则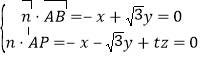 ,令
,令![]() ,得
,得![]() ,
,
平面PBD的法向量![]() (1,0,0),
(1,0,0),
因为二面角A﹣PB﹣D的余弦值为![]() ,
,
所以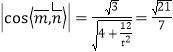 ,
,
所以![]() 或
或![]() (舍),
(舍),
则![]()
∴![]() ,
,
∴EC与平面PAB所成角![]() 的正弦值为
的正弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,已知∠A= ![]() ,∠B=
,∠B= ![]() ,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED=
,AB=6,在AB边上取点E,使得BE=1,连接EC,ED.若∠CED= ![]() ,EC=
,EC= ![]() .
. 
(Ⅰ)求sin∠BCE的值;
(Ⅱ)求CD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆x2+y2﹣2x+10y﹣24=0和 x2+y2+2x+2y﹣8=0
(1)判断两圆的位置关系;(2)求公共弦所在的直线方程及公共弦的长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+ ![]() ),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
),f′(x)是f(x)的导函数,则函数y=2f(x)+f′(x)的一个单调递减区间是( )
A.[ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非零向量 ![]() ,
, ![]() 的夹角为
的夹角为 ![]() ,且满足|
,且满足| ![]() |=λ|
|=λ| ![]() |(λ>0),向量组
|(λ>0),向量组 ![]() ,
, ![]() ,
, ![]() 由一个
由一个 ![]() 和两个
和两个 ![]() 排列而成,向量组
排列而成,向量组 ![]() ,
, ![]() ,
, ![]() 由两个
由两个 ![]() 和一个
和一个 ![]() 排列而成,若
排列而成,若 ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() 所有可能值中的最小值为4
所有可能值中的最小值为4 ![]() 2 , 则λ= .
2 , 则λ= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海警基地码头O的正东方向40海里处有海礁界碑M,过点M且与OM成![]() (即北偏西
(即北偏西![]() )的直线l在在此处的一段为领海与公海的分界线(如图所示),在码头O北偏东
)的直线l在在此处的一段为领海与公海的分界线(如图所示),在码头O北偏东![]() 方向领海海面上的A处发现有一艘疑似走私船(可疑船)停留. 基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从O处即刻出发,按计算确定方向以可疑船速度的2倍航速前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在P处恰好截获可疑船.
方向领海海面上的A处发现有一艘疑似走私船(可疑船)停留. 基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从O处即刻出发,按计算确定方向以可疑船速度的2倍航速前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在P处恰好截获可疑船.
(1)如果O和A相距6海里,求可疑船被截获处的点P的轨迹;
(2)若要确保在领海内捕获可疑船(即P不能在公海上).则![]() 、
、![]() 之间的最大距离是多少海里?
之间的最大距离是多少海里?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求BD1与平面A1BC1所成角的正弦值.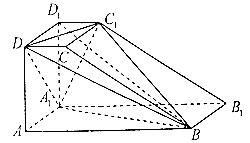
查看答案和解析>>
科目:高中数学 来源: 题型:
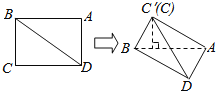
【题目】如图所示,在矩形ABCD中,![]() ,
,![]() 沿对角线将
沿对角线将![]() 折起,使点C移到
折起,使点C移到![]() 点,且C点在平面ABD的射影O恰在AB上.
点,且C点在平面ABD的射影O恰在AB上.
(1)求证:![]() 平面ACD;
平面ACD;
![]() 求直线AB与平面
求直线AB与平面![]() D所成角的正弦值.
D所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com