
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)根据题中条件运用基本量之间的关系求解;(2)借助题设条件运用直线和椭圆的位置关系建立坐标之间的关系,再用坐标之间的关系分析推证即可.
试题解析:(1)解:由题意得椭圆![]() 的焦点在
的焦点在![]() 轴上………………………………1分
轴上………………………………1分
∵椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点,∴
对称的图形过坐标原点,∴![]() ,………………………………3分
,………………………………3分
∵![]() ,∴
,∴![]() ,解得
,解得![]() …………………………………………………………4分
…………………………………………………………4分
∴椭圆![]() 的方程为
的方程为![]() .………………………………………………5分
.………………………………………………5分
(2)证明:易知直线![]() 的斜率必存在,设直线
的斜率必存在,设直线![]() 的方程为
的方程为![]() ,
,
代入![]() 得
得![]() ,
,
由![]() 得,
得,![]() .…………………………7分
.…………………………7分
设![]() ,
,![]() ,则
,则
![]() ,
,![]() ,……………………………………8分
,……………………………………8分
则直线![]() 的方程为
的方程为![]() ,
,
令![]() 得:
得:![]()
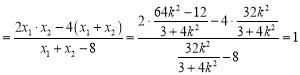 ,
,
∴直线![]() 过定点
过定点![]() ,又
,又![]() 的右焦点为
的右焦点为![]() ,∴直线
,∴直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .…………12分
.…………12分


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,长轴在
的中心在坐标原点,长轴在![]() 轴上,
轴上,![]() 分别在其左、右焦点,
分别在其左、右焦点,![]() 在椭圆上任意一点,且
在椭圆上任意一点,且![]() 的最大值为1,最小值为
的最大值为1,最小值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的右顶点,直线
的右顶点,直线![]() 是与椭圆交于
是与椭圆交于![]() 两点的任意一条直线,若
两点的任意一条直线,若![]() ,证明直线
,证明直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(1)若![]() ,
, ![]() 为直线
为直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(2)若直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,
初赛采用选手选一题答一题的方式进行,每位选手最多有![]() 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对![]() 题或答错
题或答错![]() 题即终止其初赛的比赛,答对
题即终止其初赛的比赛,答对![]() 题者直接进入决赛,答错
题者直接进入决赛,答错![]() 题者则被淘汰.已知选手甲答题的正确率为
题者则被淘汰.已知选手甲答题的正确率为![]() .
.
(1) 求选手甲可进入决赛的概率;
(2) 设选手甲在初赛中答题的个数为![]() ,试写出
,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等式:sin25°+cos235°+sin 5°cos 35°=![]() ,
,
sin215°+cos245°+sin 15°cos 45°=![]() ,sin230°+cos260°+sin 30°·cos 60°=
,sin230°+cos260°+sin 30°·cos 60°=![]() ,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
,…,由此归纳出对任意角度θ都成立的一个等式,并予以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解大学生观看浙江卫视综艺节目“奔跑吧兄弟”是否与性别有关,一所大学心理学教师从该校学生中随机抽取了50人进行问卷调查,得到了如下的列联表:
喜欢看“奔跑吧兄弟” | 不喜欢看“奔跑吧兄弟” | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
若该教师采用分层抽样的方法从50份问卷调查中继续抽查了10份进行重点分析,知道其中喜欢看“奔跑吧兄弟”的有6人.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜欢看“奔跑吧兄弟”节目与性别有关?说明你的理由;
的把握认为喜欢看“奔跑吧兄弟”节目与性别有关?说明你的理由;
(3)已知喜欢看“奔跑吧兄弟”的10位男生中,![]() 还喜欢看新闻,
还喜欢看新闻,![]() 还喜欢看动画片,
还喜欢看动画片,![]() 还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求
还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
P(χ2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com