
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 经过曲线
经过曲线![]() 与
与![]() 轴的交点.
轴的交点.
(1)求圆![]() 的方程;
的方程;
(2)已知过坐标原点![]() 的直线
的直线![]() 与圆
与圆![]() 交
交![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】试题分析:
(1)先求出曲线与![]() 轴的交点为
轴的交点为![]() ,再根据圆心在直线
,再根据圆心在直线![]() ,由待定系数法可求得圆的方程为
,由待定系数法可求得圆的方程为![]() .(2)由题意设直线
.(2)由题意设直线![]() 的方程为
的方程为![]() ,代入圆方程消去
,代入圆方程消去![]() 整理得
整理得![]() ,设
,设![]() ,由根与系数的关系可得
,由根与系数的关系可得![]() .又由
.又由![]() ,得
,得![]() ,消去
,消去![]() 后可解得
后可解得![]() 或
或![]() ,从而可得到直线方程.
,从而可得到直线方程.
试题解析:
(1)在![]() 中,
中,
令![]() ,得
,得![]() ,
,
解得![]() 或
或![]() ,
,
所以曲线![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为![]() .
.
设圆![]() 的方程为
的方程为![]() ,
,
依题意得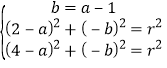 ,
,
解得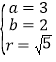 ,
,
所以圆![]() 的方程为
的方程为![]() .
.
(2)解法一:
由题意知直线![]() 的斜率显然存在,故设直线
的斜率显然存在,故设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由![]() 消去
消去![]() 整理得
整理得
![]() ,
,
因为直线![]() 与圆
与圆![]() 交
交![]() 两点,
两点,
所以![]() .
.
设![]() ,
,
则![]()
因为![]() ,
,
所以![]() ,
,
所以![]()
解得![]() 或
或![]() ,
,
经检验得![]() 或
或![]() 满足
满足![]() ,
,
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.
解法二:
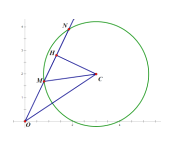
如图取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
则![]()
设![]()
由![]() ,得
,得![]()
由![]()
所以![]()
解得![]()
所以圆心![]() 到直线
到直线![]() 的距离等于2,
的距离等于2,
设直线![]() 的方程为
的方程为![]() ,即
,即![]()
所以![]() ,
,
解得![]() 或
或![]() ,
,
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.
解法三:
设直线![]() 的倾斜角为
的倾斜角为![]() ,则直线
,则直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
把![]() 代入
代入![]() 并整理得:
并整理得:
![]()
设![]() 对应的参数分别为
对应的参数分别为![]() ,
,
则![]()
因为![]() ,
,
所以![]() ,
,![]() ,
,
所以![]()
所以![]() ,
,
所以![]()
所以![]() ,
,
所以![]() 或
或![]()
所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知![]() ,函数F(x)=min{2|x1|,x22ax+4a2},
,函数F(x)=min{2|x1|,x22ax+4a2},
其中min{p,q}=![]()
(Ⅰ)求使得等式F(x)=x22ax+4a2成立的x的取值范围;
(Ⅱ)(ⅰ)求F(x)的最小值m(a);
(ⅱ)求F(x)在区间[0,6]上的最大值M(a).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y= 4cos2x+4![]() sinxcosx-2,(x∈R)
sinxcosx-2,(x∈R)
(1)求函数的最小正周期;
(2)求函数的最大值及其相对应的x值;
(3)写出函数的单调增区间;
(4)写出函数的对称轴
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 是以原点O为中心、
是以原点O为中心、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以O为顶点、
是以O为顶点、![]() 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线![]() 和
和![]() 的交点且
的交点且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.

(1)求曲线![]() 和
和![]() 的方程;
的方程;
(2)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问![]() 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.在党和政府强有力的抗疫领导下,我国控制住疫情后,一方面防止境外疫情输入,另一方面逐步复工复产,减轻经济下降对企业和民众带来的损失.为降低疫情影响,某厂家拟在2020年举行某产品的促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按
为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按![]() 元来计算)
元来计算)
(1)将2020年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com