
【题目】已知:β∈(0, ![]() ),α∈(
),α∈( ![]() ,
, ![]() )且cos(
)且cos( ![]() ﹣α)=
﹣α)= ![]() ,sin(
,sin( ![]() +β)=
+β)= ![]() ,求:cosα,cos(α+β)
,求:cosα,cos(α+β)
【答案】解:∵ ![]() <α<
<α< ![]() ,∴﹣
,∴﹣ ![]() <
< ![]() ﹣α<0.
﹣α<0.
∵cos( ![]() ﹣α)=
﹣α)= ![]() ,∴sin(
,∴sin( ![]() ﹣α)=﹣
﹣α)=﹣ ![]() ,
,
∴cos α=cos[ ![]() ﹣(
﹣( ![]() ﹣α)]
﹣α)]
=cos ![]() cos(
cos( ![]() ﹣α)+cos
﹣α)+cos ![]() sin(
sin( ![]() ﹣α)
﹣α)
= ![]()
![]() +
+ ![]() (﹣
(﹣ ![]() )
)
= ![]() .
.
又∵0<β< ![]() ,∴
,∴ ![]() <
< ![]() +β<π.
+β<π.
∵sin( ![]() +β)=
+β)= ![]() ,∴cos(
,∴cos( ![]() +β)=
+β)= ![]() Z,
Z,
∴cos(α+β)=sin[ ![]() +(α+β)]=sin[(
+(α+β)]=sin[( ![]() +β)﹣(
+β)﹣( ![]() ﹣α)]
﹣α)]
=sin( ![]() +β)cos(
+β)cos( ![]() ﹣α)﹣cos(
﹣α)﹣cos( ![]() +β)sin(
+β)sin( ![]() ﹣α)
﹣α)
= ![]()
![]() ﹣(﹣
﹣(﹣ ![]() )(﹣
)(﹣ ![]() )
)
=﹣ ![]() .
.
【解析】根据两角和与差的正弦余弦函数同角三角函数间的基本关系即可求出.
【考点精析】本题主要考查了两角和与差的余弦公式的相关知识点,需要掌握两角和与差的余弦公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)记线段![]() 的中点为
的中点为![]() ,在平面
,在平面![]() 内过点
内过点![]() 作一条直线与平面
作一条直线与平面![]() 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,cos2B﹣5cos(A+C)=2.
(1)求角B的值;
(2)若cosA= ![]() ,△ABC的面积为10
,△ABC的面积为10 ![]() ,求BC边上的中线长.
,求BC边上的中线长. 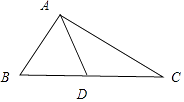
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个非零向量 ![]() 、
、 ![]() 不共线.
不共线.
(1)若 ![]() =
= ![]() +
+ ![]() ,
, ![]() =2
=2 ![]() +8
+8 ![]() ,
, ![]() =3(
=3( ![]() ﹣
﹣ ![]() ),求证:A、B、D三点共线;
),求证:A、B、D三点共线;
(2)求实数k使k ![]() +
+ ![]() 与2
与2 ![]() +k
+k ![]() 共线.
共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数y=2sin(2x﹣ ![]() )的一条对称轴是x=
)的一条对称轴是x= ![]() ;
;
②函数y=tanx的图象关于点( ![]() ,0)对称;
,0)对称;
③正弦函数在第一象限为增函数
④存在实数α,使 ![]() sin(α+
sin(α+ ![]() )=
)= ![]()
以上四个命题中正确的有(填写正确命题前面的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() .
.
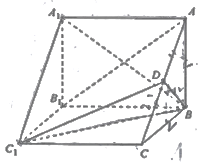
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com