Question

（本题满分12分）

 今年十一黄金周，记者通过随机询问某景区110名游客对景区的服务是否满意，得到如下的列联表：

性别与对景区的服务是否满意　　单位：名

	男	女	总计
满意	50	30	80
不满意	10	20	30
总计	60	50	110

（1）从这50名女游客中按对景区的服务是否满意采取分层抽样，抽取一个容量为5的样本，问样本中满意与不满意的女游客各有多少名？

（2）从（1）中的5名女游客样本中随机选取两名作深度访谈，求选到满意与不满意的女游客各一名的概率；

（3）根据以上列联表，问有多大把握认为“游客性别与对景区的服务满意”有关

注：

临界值表：

P()	0.05	0.025	0.010	0.005
	3.841	5.024	6.635	7.879

 

Answer 1

【答案】

解：（1）样本中满意的女游客为3名，样本中不满意的女游客为2名。

（2） 。

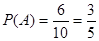（3）有99％的把握认为：该景区游客性别与对景区的服务满意有关。

【解析】

试题分析：（I）每个个体被抽取的概率为 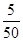，根据分层抽样，即可得样本中满意的女游客，样本中不满意的女游客的人数；

（II）确定从这5名游客中随机选取两名的等可能事件的个数，其中事件A“选到满意与不满意的女游客各一名”包含6个基本事件，即可求得概率；

（III）由列联表，计算K²的值，根据P（K²＞6.635）=0.010，即可得到结论．

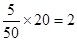解：（1）根据分层抽样可得：样本中满意的女游客为名，样本中不满意的女游客为名。

（2）记样本中对景区的服务满意的3名女游客分别为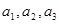，对景区的服务不满意的2名女游客分别为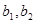。从5名女游客中随机选取两名，共有10个基本事件，分别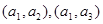为：，，，，；其中事件A：选到满意与不满意的女游客各一名包含了6个基本事件，分别为：，，

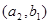
所以所求概率 。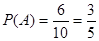

（3）假设：该景区游客性别与对景区的服务满意无关，则应该很小。

根据题目中列联表得：

由可知：有99％的把握认为：该景区游客性别与对景区的服务满意有关。

考点：本试题主要考查了分层抽样，考查等可能事件概率的求法，考查独立性检验知识，考查学生的计算能力，属于中档题．

点评：根据已知条件理解古典概型的概率中总的基本事件数从而求解概率的值，对于分层抽样的等概率抽样即为样本容量与总体的比值。